Analýza dat v neurologii LXXIII. Problematika interpretace Pearsonova korelačního koeficientu
Autoři:
L. Dušek; T. Pavlík; J. Jarkovský
; J. Koptíková
Působiště autorů:
Institut biostatistiky a analýz, LF MU, Brno
Vyšlo v časopise:
Cesk Slov Neurol N 2019; 82(1): 113-117
Kategorie:
Okénko statistika
Pearsonova korelačního koeficientu
Tímto dílem našeho seriálu zakončíme výklad parametrické korelační analýzy, jejímž primárním cílem je odhadnout hodnotu kovariance či Pearsonova korelačního koeficientu. Pearsonův korelační koeficient (značíme r nebo R) jsme v minulých dvou dílech hodnotili jako míru obecněji lépe využitelnou než kovariance, zejména proto, že jde o statistiku standardizovanou, nabývající hodnoty pouze v intervalu od – 1 do +1. Krajní hodnoty přitom značí absolutní korelaci, kdy hodnoty spojitých proměnných leží přesně na přímce (ukázku této situace mezi proměnnými X a Y znázorňují příklady 1a– b). Takovou extrémní závislost samozřejmě při běžných korelačních analýzách na vzorku subjektů nenajdeme, v důsledku variability hodnot se body proměnných X a Y přímkovému vztahu pouze blíží, jak ukazují příklady 1d– f. Lineární vztah obou veličin, tedy přímka popisující závislost, je zde obdobou míry polohy a výstupem korelační analýzy pak je jistá míra ,,těsnosti” hodnot proměnných vzhledem k této přímce. Je-li výskyt hodnot jedné proměnné náhodný vůči proměnné druhé, hovoříme o jejich nezávislosti, resp. o nulové korelaci (ukázka na příkladu 1c).

Hodnoty Pearsonova korelačního koeficientu rovné – 1 nebo +1 ukazují na deterministický vztah obou proměnných, kdy z hodnoty X lze přesně vypočítat odpovídající hodnotu Y. Typickým příkladem jsou např. kalibrační křivky laboratorních úloh, kdy z hodnoty absorbance vzorku počítáme hodnotu koncentrace látky apod. Obecně však vždy platí, že jak korelace, tak kalibrace hodnotí vztah dvou spojitých proměnných. V případě Pearsonovy korelace jde o vztah přímkový, lineární. Rozdíl je pouze v interpretaci, neboť u korelace hodnotíme pouze obecný vztah a jeho sílu, přičemž k oběma proměnným přistupujeme interpretačně stejně a nepředjímáme jejich příčinný vztah. U kalibrace naopak směr vztahu proměnných předjímáme a také rozlišujeme pozici proměnných X a Y, tedy že jedna proměnná závisí na druhé.
Výše uvedeným textem a příkladem 1 nechceme pouze opakovat základy korelační analýzy vysvětlené v předchozích dílech. Chceme tím zdůraznit, že smysluplná interpretace Pearsonovy korelace se týká pouze přímkových vztahů mezi dvěma spojitými veličinami. To je velmi podstatné omezení, neboť zejména v biologii a medicíně jsou nelineární vztahy proměnných velmi časté. Jak dokládá příklad 2, v těchto situacích může standardní korelační analýza vést k nízkým hodnotám korelačního koeficientu a k chybnému potvrzení nezávislosti obou proměnných. Zatímco analýza znázorněná na příkladu 2a je správným potvrzením neexistence lineárního vztahu X a Y, příklad 2b ukazuje silný parabolický vztah obou proměnných, kde hodnota korelačního koeficientu nevede ke smysluplné interpretaci. Přitom číselně hodnotu korelace u takových závislosti spočítat lze, ale jen z publikované hodnoty R nelze nelineární vztah rozpoznat. Problémem není samotný výpočet, ale interpretace výsledku. Proto je tak zásadní doplnit odhad hodnoty korelace grafickým znázorněním výsledku.

Grafická inspekce vztahu X a Y by při korelační analýze měla být povinná ještě z jednoho velmi závažného důvodu. Lze tak snadno odhalit problémy a anomálie v rozdělení hodnot korelovaných proměnných. Připomeňme, že Pearsonova korelace je parametrickou analýzou vyžadující normální rozdělení u obou proměnných vstupujících do analýzy. Silná asymetrie v rozdělení hodnot X nebo Y, vícemodální rozdělení či výskyt odlehlých hodnot vždy závažným způsobem ovlivňují hodnotu korelačního koeficientu a mohou vést k nesmyslným závěrům analýzy. Tyto skutečnosti jsme se pokusili znázornit na příkladech 3– 5.


Příklad 3 znázorňuje korelaci proměnných X a Y, přičemž obě proměnné mají téměř učebnicové normální rozdělení hodnot (znázorněné jako histogramy na boku korelačního diagramu). Odhad hodnoty korelačního koeficientu v tomto případě nebude rozdělením hodnot zkreslený.
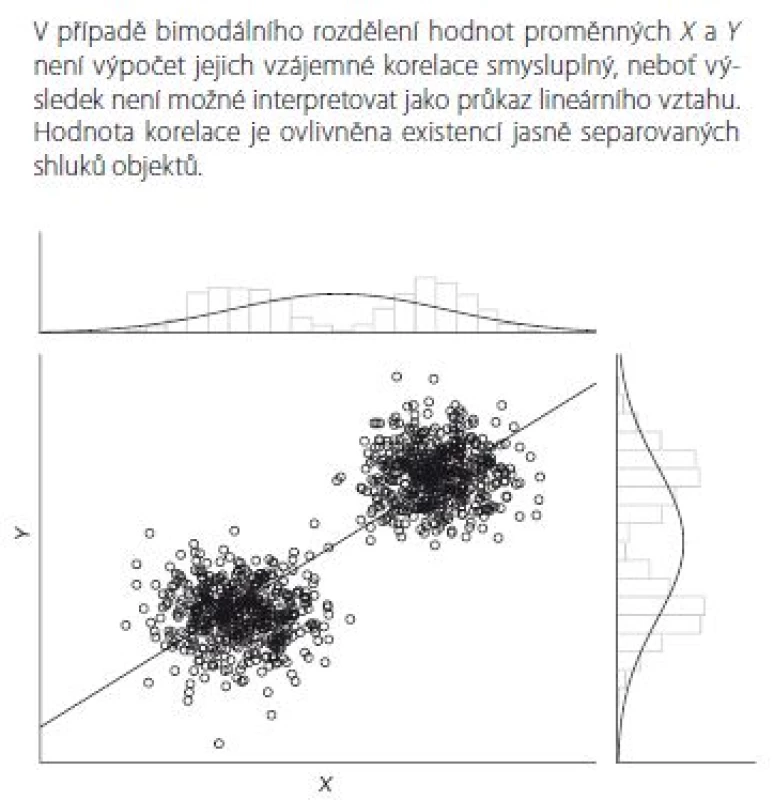
Příklad 4 ukazuje situaci, kdy vstupní data X a Y vykazují silné bimodální rozdělení (rozdělení s dvěma frekvenčními vrcholy – modusy) v důsledku výskytu dvou vzájemně separovaných shluků objektů. Je patrné, že pokud by korelační analýza byla provedena pro jednotlivé shluky objektů odděleně, vedla by k závěru o neexistenci vztahu mezi X a Y. Celková analýza spojených dat avšak povede k relativně vysoké kladné hodnotě korelačního koeficientu, která tak bude odrážet pouze existenci shluků objektů. Graf na příkladu 4 dokládá, že existence přímky mezi hodnotami X a Y není reálným obrazem jejich závislosti. Spíše než na odhad R by se analýza měla zaměřit na objasnění důvodu existence shluků hodnot. Objekty náležející různým shlukům mohou mít řadu rozdílných charakteristik, jejichž poznání bude pro analýzu podstatné. Avšak takto výrazné bimodální rozdělení hodnot může být i důsledkem chybného vzorkovacího plánu (výběr objektů nepokryl reprezentativně oblast středních hodnot X a Y) nebo může být způsobeno nějakým pozaďovým faktorem, jehož vliv subjekty významně odlišuje.
Příklad 5 znázorňuje nejextrémnější situaci, při které míra zkreslení odhadu korelačního koeficientu dělá jeho interpretaci velmi problematickou. Je patrné, že rozdělení hodnot proměnných X a Y zahrnuje několik silně odlehlých hodnot; předpoklad normality rozdělení veličin je zde nepochybně silně porušen. Výsledkem bude vysoká, avšak obtížně interpretovatelná hodnota korelačního koeficientu. Takový vliv může mít dokonce i jedna odlehlá hodnota, která je způsobena např. překlepem při zadávání vstupních dat do souboru.
Je zřejmé, že hodnota korelačního koeficientu je silně závislá na rozdělení hodnot vstupujících proměnných, a odhad korelace by proto měl být vždy založen na poctivé kontrole vstupních dat. Čtenáři si jistě nyní kladou otázku, jak může jedna odlehlá hodnota proměnné X nebo Y zkreslit odhad korelace tak, že bude nesmyslná. Vysvětlením je samotný vztah pro výpočet R, který zde připomínáme:

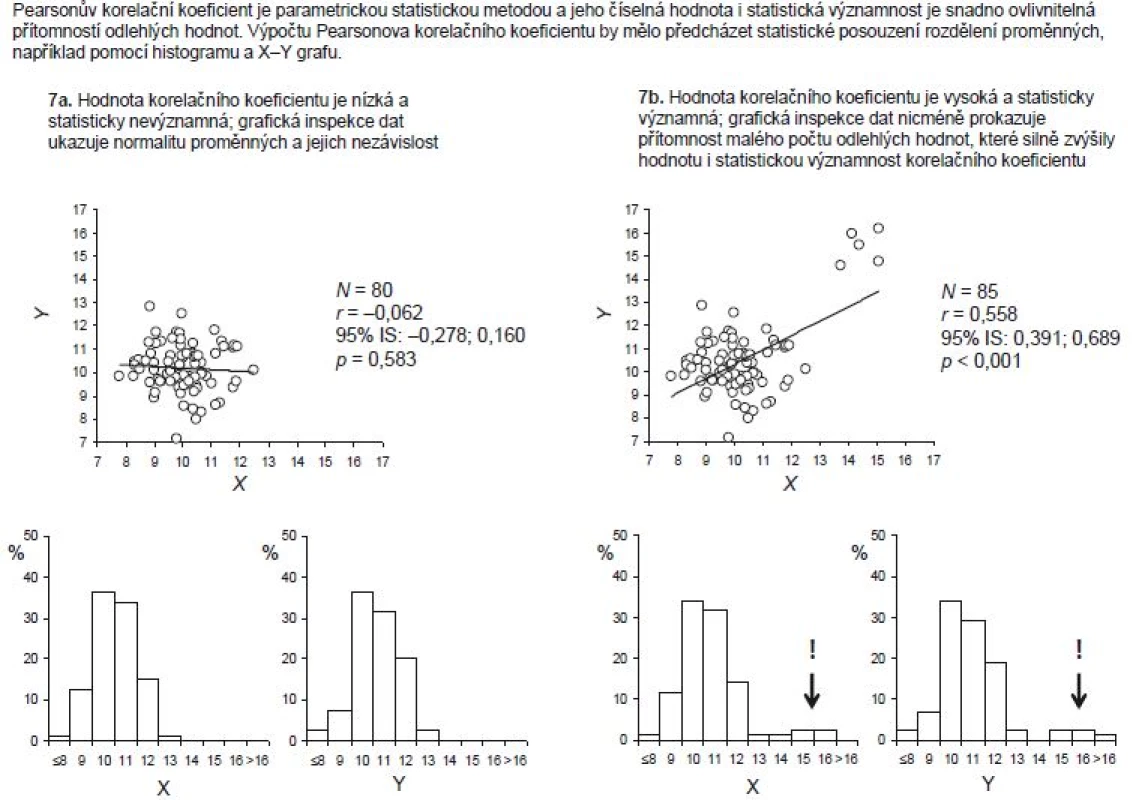
Extrémně vysoká hodnota xi nebo yi nutně zvýší hodnotu čitatele, a tedy i hodnotu výsledného R. Skutečně se tak může stát, že v důsledku jedné nereálné hodnoty budeme publikovat vysokou korelaci mezi proměnnými, a ona přitom vůbec nebude v datech existovat (viz dokumentace na příkladech 6 a 7, zejména ukázka na příkladu 6c. I proto bývá korelační koeficient v odborné literatuře často označován za nejvíce zneužívanou statistiku či za statistiku „zranitelnou“ vstupními daty.
Tímto bohužel výčet úskalí korelační analýzy nekončí. Výklad uzavřeme komentářem, jak výsledek korelace ovlivňuje i sama velikost vzorku. Již v minulém díle seriálu jsme dokládali, že statistickou významnost korelačního koeficientu ovlivňuje nejen jeho absolutní hodnota, ale i velikost vzorku N, na kterém byl koeficient odhadnut. To vyplývá ze vztahu pro výpočet testové statistiky pro posouzení statistické významnosti R, která má Studentovo rozdělení t a N – 2 stupně volnosti:
Je zřejmé, že vysoká hodnota N numericky zvýší hodnotu statistiky t, a tím povede k průkazu statistické významnosti R, tj. k zamítnutí nulové hypotézy R = 0. U velmi velkých vzorků tak může být za statisticky významný prokázán i korelační koeficient s nízkou hodnotou, tedy numericky blízký nule. Tuto skutečnost ilustruje příklad 8, ze kterého je patrné, že i velmi nízká hodnota R může dosáhnout prokazatelné statistické významnosti, je-li získána analýzou velkého vzorku hodnot (příklad 8d: R = 0,078; N = 1000; p = 0,015). A naopak relativně vysoká hodnota R nemusí být prokázána jako statisticky významná, pokud jde o malý vzorek hodnot (příklad 8a: R = 0,699; N = 7; p = 0,081). K interpretaci statistické významnosti R je tedy nutné přistupovat i s ohledem na absolutní hodnotu R. Samotné konstatování, že hodnota R je statisticky významná, nemusí nutně znamenat, že jde o vysokou korelaci prokazující jasný přímkový vztah X a Y.

prof. RNDr. Ladislav Dušek, Ph.D.
Institut biostatistiky a analýz, LF MU, Brno
e‑mail: dusek@iba.muni.cz
Štítky
Dětská neurologie Neurochirurgie NeurologieČlánek vyšel v časopise
Česká a slovenská neurologie a neurochirurgie

2019 Číslo 1
Nejčtenější v tomto čísle
- Lehká mozková poranění – konsenzuální odborné stanovisko České neurologické společnosti ČLS JEP
- Chronický subdurální hematom
- Ketogenní dieta – účinná nefarmakologická léčba dětské a adolescentní epilepsie
- Oligoklonální IgG a volné lehké řetězce – srovnání izoelektrické fokusace v agarózovém a polyakrylamidovém gelu


