Analýza dat v neurologii. IV.
Variabilita měření není vždy „chyba“
Autoři:
Ladislav Dušek; Tomáš Pavlík; Jana Koptíková
Působiště autorů:
Institut biostatistiky a analýz, Masarykova univerzita, Brno
Vyšlo v časopise:
Cesk Slov Neurol N 2007; 70/103(4): 446-449
Kategorie:
Webové okénko
V předchozím díle této řady jsme se věnovali správnému výběru statistik středu, tedy možným reprezentantům naměřených hodnot, jako jsou hlavně medián a průměr. V biologii a medicíně však nevystačíme pouze s ukazatelem středu, tento musí být vždy doplněn ukazatelem variability hodnot. Nutno říci, že naštěstí nevystačíme, neboť žijeme v rozmanitém světě a každý hodnocený jedinec je individualita poskytující i za zcela stejných podmínek mírně odlišný výsledek měření. Hovoříme o variabilitě primárních dat, která je vyjadřována tzv. mírami rozptýlenosti. Variabilita dat je neoddělitelnou vlastností biologických i klinických znaků, někdy i významnější než průměr nebo medián. Některé znaky mají přirozeně větší nebo menší variabilitu, kterou ovlivňují genetické a fenotypové rozdíly mezi jedinci, podmínky měření a samozřejmě také standardizace metodiky měření.
Již v úvodu této kapitoly tedy odlišujme:
- variabilitu primárních dat, která vypovídá o rozptýlenosti hodnot ve výběrové populaci a je odhadem situace v cílové populaci
- variabilitu související s odhady vybraných statistik (ukazatelů), např. průměru.
Pouze v druhém případě můžeme hovořit o nepřesnosti nebo chybě měření. Variabilitu primárních dat naopak musíme respektovat jako atribut vyžadující adekvátní vyjádření a interpretaci. Měříme-li opakovaně koncentraci látky v kádince roztoku, pak jsou rozdílné hodnoty měření jistě výrazem naší chyby a budeme mít tendenci je metodicky minimalizovat. Sledujeme-li však tělesnou výšku nějaké skupiny pacientů, pak rozdíly mezi jedinci v souboru dat určitě nebudeme považovat za odstranitelný problém. Budeme-li následně na takto naměřeném souboru odhadovat průměrnou tělesnou výšku, nepřesnost tohoto odhadu již bude mít charakter chyby.
Variabilita dat určuje naše možnosti měření a poznání. Více variabilní znaky je těžší měřit a je také problematičtější u nich prokazovat rozdíly například mezi zdravými a nemocnými jedinci. Primárně („přírodně“) variabilnější znaky vedou logicky k variabilnějším odhadům středových hodnot a k dosažení určité přesnosti zde potřebujeme větší počty měření.
Úkolem analýzy dat je variabilitu změřit a vyjádřit vhodnými ukazateli, které ovšem mohou být stejné pro primární data i pro chybovost odhadů. Základní pravidla se přitom nijak neliší od již probírané problematiky odhadu středových hodnot. Lze tedy v zásadě vybírat mezi dvěma strategiemi:
I. Robustní statistiky rozptýlenosti nevyžadují žádné předpoklady, kromě seřazení hodnot podle velikosti. Tyto tzv. pořadové statistiky typicky doplňují medián jako ukazatel středové tendence. Na výběr máme v této kategorii několik možností:
- Jistým extrémem je vykazování přímo maximální a minimální hodnoty, případně jejich rozdílu, který se nazývá variační rozpětí. Tímto sice vykazujeme velmi pravdivě rozsah naměřených hodnot, otázka je však nakolik věrohodně. Minima a maxima totiž zahrnují i odlehlé nebo hraniční hodnoty, které nemusí být v dané situaci vůbec reprezentativní.
- Velmi rozšířenými statistikami jsou tzv. percentily jako statistiky, které procenticky vyjadřují pořadí daného čísla v souboru. Pod 20% percentilem tak leží 20 % všech hodnot, medián je 50 % percentil atd. Alternativním termínem pro percentil je empirický kvantil, který je definován pro určitou pravděpodobnost výskytu menších hodnot. Empirický kvantil q0,25 tak odpovídá 25 % percentilu. Pro kvantily q0,25 a q0,75 se používá specifický termín spodní a horní kvartil.
- Pro praktika je podstatné především to, že percentily (kvantily) lze určit vždy, jsme–li schopni seřadit čísla podle velikosti. Fungují tedy velmi dobře i pro ordinální stupnice. Kvantily také velmi dobře vyjadřují rozptýlenost primárních dat bez nadbytečného počítání a předpokladů. V praxi se tak často používají odhady 5 % a 95 % kvantilu jako jakési „rozumné“ minimum a maximum.
II. Parametrické statistiky rozptýlenosti, jejichž výpočet je možný pouze za předpokladu, že rozložení hodnot odpovídá určitému modelovému typu. Nejtypičtějším příkladem je předpoklad zcela symetrického normálního rozložení (tzv. Gausova křivka) a od něj odvozený odhad rozptylu (standardně značen s2) a jeho druhé odmocniny – směrodatné odchylky (značeno s).
- Odmocnění rozptylu je nezbytné, abychom dostali metriku v jednotkách měřených hodnot. Rozptyl je definován jako „průměrná suma čtverců vzdálenosti každé naměřené hodnoty od průměru“, a je tedy v jednotkách osy X na druhou mocninu. Naopak směrodatnou odchylku lze odečítat od průměru a platí, že při splnění předpokladu normálního rozložení téměř 100 % hodnot leží v rozsahu průměr 3s.
Obecně platí, že s parametrickými ukazateli variability lze více pracovat než s pořadovými statistikami, ale pouze při splnění předpokladu normálního rozložení. Rozptyl a směrodatná odchylka jsou použitelné pouze tam, kde je oprávněné použití aritmetického průměru. Asymetrie rozložení hodnot nebo odlehlé hodnoty interpretaci těchto statistik zcela znehodnotí.
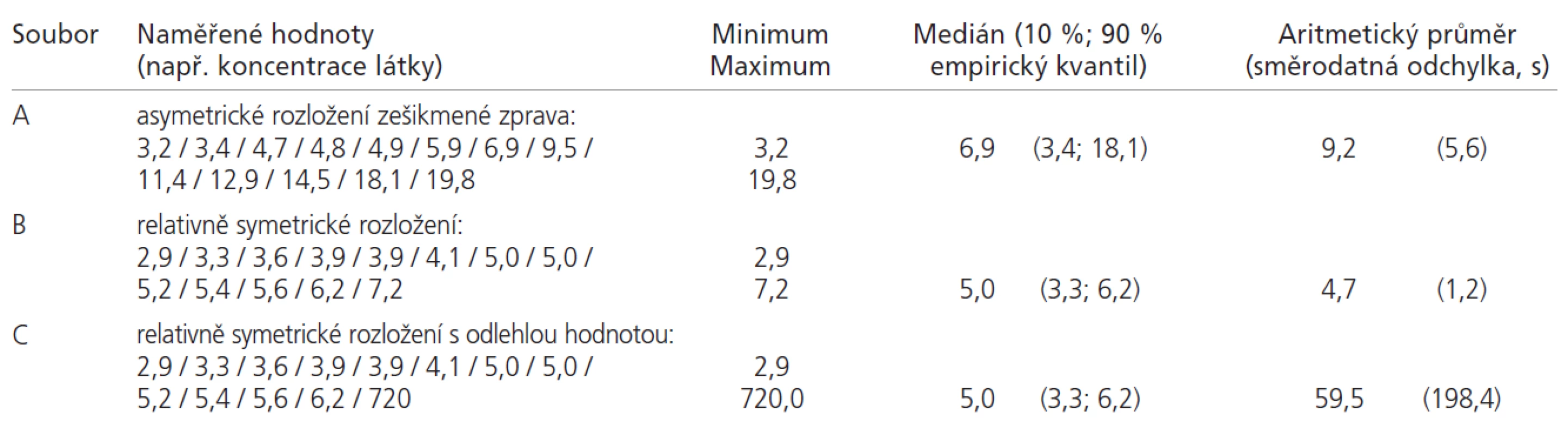
Jako příklad použijme data v tab 1. Prezentace tří rozdílných souborů dat jednoznačně ukazuje, že pořadové statistiky lze bezpečně použít kdykoli. Rozptýlenost vyjádřená pomocí 10 % a 90 % percentilu odfiltrovala i odlehlou hodnotu v souboru C. Naopak je zřejmé, že rostoucí asymetrie rozložení a odlehlá hodnota výrazně zvyšují hodnotu směrodatné odchylky, kterou již nelze smysluplně interpretovat. U souboru C se totiž hranice intervalu průměr 3s dostávají hluboce do záporných hodnot, což by u koncentrací jistě nebylo možné. Příliš velká hodnota směrodatné odchylky tak signalizuje asymetrii rozložení nebo odlehlé hodnoty, a zpochybňuje tím i použití aritmetického průměru jako ukazatele středu. Těmto problémům se lze snadno vyhnout použitím mediánu a příslušných kvantilů.
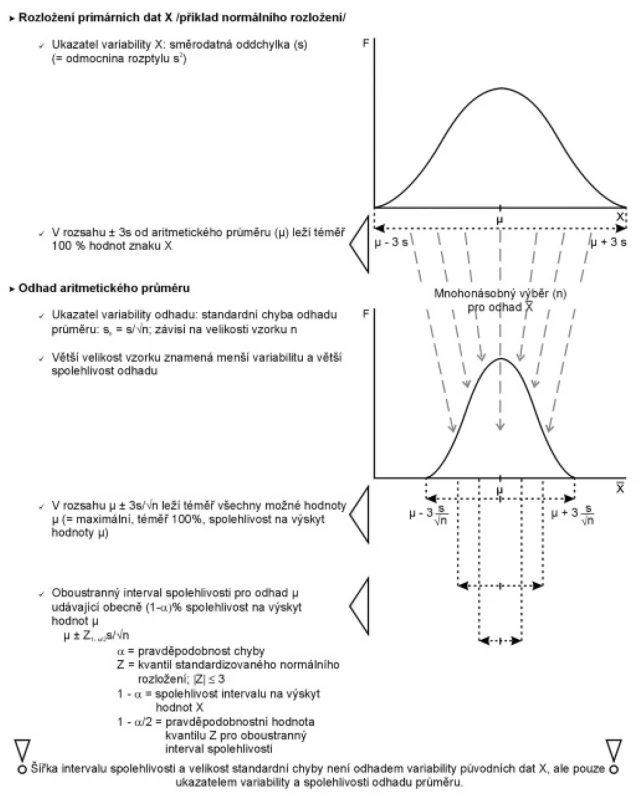
Výše uvedenou sumarizaci primárních dat je nutno odlišit od provádění odhadů a vyjadřování jejich spolehlivosti. Tuto novou kvalitu schematicky popisuje obr. 1. Opakovaným odhadem aritmetického průměru z téhož souboru dat získáváme výběrové rozložení těchto odhadovaných průměrů se vzorkem n. A v tomto rozložení (které je definičně také symetrické jako u primárních dat) je směrodatná odchylka nahrazena tzv. standardní chybou odhadu průměru se.
Platí jednoduchý vzorec se =
kde s je směrodatná odchylka počítaná na souboru n primárních naměřených hodnot.
Z tohoto vztahu lze jednoduše vyčíst následující:
- čím větší je rozptyl primárních dat, tím méně spolehlivý odhad průměru – tedy tím větší bude hodnota se
- a naopak, čím větší vzorek použijeme, tím větší přesnosti a spolehlivosti odhadu průměru dosáhneme.
Standardní chyba má tedy skutečně význam „chyby“ a vyjadřuje míru nepřesnosti odhadnutého průměru. Nevyjadřuje ale variabilitu primárních dat. V publikační sumarizaci hodnot lze samozřejmě použít obě hodnoty s i se, použití standardní chyby je ale ve vztahu k odhadu průměru logičtější (uvádíme-li odhady průměru, nepopisujeme primární data, a tedy bychom měli použít se).
Vraťme se ale ještě k pojmu spolehlivost odhadu, která má i pravděpodobnostní význam. Jak schematicky uvádí i obr. 1, v rozsahu průměr 3se leží téměř 100 % všech možných odhadů průměru. Pokud tyto hranice o něco zúžíme (tedy použijeme menší násobek než 3), získáme tzv. interval spolehlivosti odhadu průměru. Jeho správná interpretace je následující: při opakovaném provádění odhadu za stejných podmínek se pouze v 1 – a % případů můžeme dostat mimo hranice dané tímto intervalem. Běžná hodnota pro a je 5 % nebo 1 % a hovoříme tedy o 95 % a 99 % intervalu spolehlivosti. A opět jako standardní chyba, ani interval spolehlivosti nevyjadřuje variabilitu primárních dat, ale pouze spolehlivost odhadu průměru. Na příkladu symetrického souboru B z tab. 1 uvádíme v tab. 2 různé možnosti práce s těmito statistikami a jejich prezentaci.

Podobně jako pro aritmetický průměr lze počítat intervaly spolehlivosti pro jakékoli další odhady statistik, avšak za použití jiných modelových rozložení. Tato rozložení i vzorce lze snadno dohledat v tabulkách, princip zůstává stejný jako zde prezentovaného odhadu průměru. Použitý typ rozložení představuje matematicky ověřený model a musí existovat, jinak nelze tyto výpočty smysluplně provádět. Od modelového rozložení se odvozuje určitý pravděpodobnostní kvantil, který určuje šířku intervalu spolehlivosti. Použijeme–li 97,5 % kvantil pro násobení hodnoty se, získáme 95 % oboustranný interval spolehlivosti apod. U aritmetického průměru je takto využíváno normální rozložení (kvantily se mezinárodně značí z), které u menších vzorků nahrazuje tzv. Studentovo rozložení (kvantily se znační t). Některé významné kvantily shrnuje tab. 3.

Prostor vymezený pro tento statistický seriál neumožňuje detailní popis jak výše uvedené statistiky krok po kroku spočítat. Navíc v době počítačů již možná tyto vzorce ztrácejí pro biologii a medicínu svou metodickou sílu. Avšak i biologové a lékaři musí umět již vyhodnocená data číst a interpretovat. Musíme umět interpretovat variabilitu primárních dat a variabilitu odhadů různých statistik. U problematických nebo nestandardních tvarů rozložení musíme umět zvolit robustní statistiky, při splnění podmínek modelových rozložení naopak lépe parametrické ukazatele. Nesmí se nám plést význam směrodatné odchylky a standardní chyby průměru. A konečně, spatříme-li interval spolehlivosti, musíme vědět, že jeho šířku ovlivňuje kromě primární variability znaku také velikost vzorku a nastavená hladina spolehlivosti. A že tedy nejde o přímočarý ukazatel variability dat, ale spíše o doklad kvality a spolehlivosti provedeného odhadu, například aritmetického průměru.
doc. RNDr. Ladislav Dušek, Dr.
Institut biostatistiky a analýz,
Masarykova univerzita, Brno
e-mail: dusek@cba.muni.cz
Štítky
Dětská neurologie Neurochirurgie NeurologieČlánek vyšel v časopise
Česká a slovenská neurologie a neurochirurgie

2007 Číslo 4
-
Všechny články tohoto čísla
- Cervikální dystonie
- Repetitivní transkraniální magnetická stimulace a chronický subjektivní nonvibrační tinnitus
- Hladina D-dimerů u pacientů s akutní ischemickou cévní mozkovu příhodou
- Komentář k pilotní studii autorů D. Školoudíka et al. Změny kognitivních funkcí u pacientů s akutní cévní mozkovou příhodou testovaných pomocí Mini-Mental State Examination (MMSE) a Clock Drawing Test (CDT)
- Změny kognitivních funkcí u pacientů s akutní cévní mozkovou příhodou testovaných pomocí Mini-Mental State Examination a Clock Drawing Test
- Dekompresní kraniektomie jako léčba pro krysí model „maligního“ infarktu střední mozkové tepny
- Korelace mezi indexem IgG a oligoklonálními pásy při CSF vyšetření u pacientů s roztroušenou sklerózou
- Svalová biopsie u myotonické dystrofie v éře molekulární genetiky
- Chirurgická léčba hormonálně aktivních adenomů hypofýzy
- Analýza 1 775 pacientů léčených pro trigeminální neuralgii perkutánní radiofrekvenční rizotomií
- Ovlivnění exprese mRNA genu SMN2 inhibitory histonových deacetyláz a jejich vliv na fenotyp spinální svalové atrofie I. a II. typu
- Komentář ke článku Balcer LJ, Galetta SL, Calabresi PA et al. Natalizumab reduces visual loss in patiens with relapsing multiple sclerosis. Neurology 2007; 68: 1299–1304.
- Poliomyelitis-like syndrom na podkladě klíšťové meningoencefalitidy
- Satelitní anatomický worhshop Transtemporal approaches
- Trombóza esovitého splavu – současný pohled na diagnostiku a léčbu
- Léčba spánkové apnoe malých dětí dvojúrovňovým přetlakem v dýchacích cestách
- Polykací obtíže u difuzní idiopatické kostní hyperostózy
- Hennerici MG, Daffertshofer M, Caplan LR, Szabo K (Eds). Case Studies in Stroke. Common and Uncommon Presentations. Cambridge: Cambridge University Press 2007. 272 p. ISBN 0-521-67367-4.
- Lze bez pochybností interpretovat výsledky lumbálního infuzního testu?
- Zpráva z 8. sjezdu Evropské společnosti báze lební
-
Analýza dat v neurologii. IV.
Variabilita měření není vždy „chyba“ - Webové okénko
- XVIII. neuromuskulární sympozium
- Česká a slovenská neurologie a neurochirurgie
- Archiv čísel
- Aktuální číslo
- Informace o časopisu
Nejčtenější v tomto čísle
- Cervikální dystonie
- Hladina D-dimerů u pacientů s akutní ischemickou cévní mozkovu příhodou
- Trombóza esovitého splavu – současný pohled na diagnostiku a léčbu
- Repetitivní transkraniální magnetická stimulace a chronický subjektivní nonvibrační tinnitus

