Analýza dat v neurologii
XII. Úvod do statistického usuzování – postupy a terminologie
Autoři:
L. Dušek; T. Pavlík; J. Koptíková
Působiště autorů:
Masarykova univerzita, Brno
; Institut biostatistiky a analýz
Vyšlo v časopise:
Cesk Slov Neurol N 2008; 71/104(6): 735-739
Kategorie:
Okénko statistika
Minulý díl seriálu končil doporučením, že chceme‑li používat nástroje statistického usuzování, musíme sledovat nejen metodiku výpočtu, ale také reálný význam hodnocených rozdílů (efektů). Prohlásíme‑li nějaký rozdíl za statisticky významný, vždy bychom měli vědět, z jakého důvodu jsme vůbec tento postup zvolili a jak reálně významný (důležitý) pozorovaný rozdíl je. Čtenáře jsme varovali, že samotný výpočet statistických testů nezahrnuje kontrolu věcného významu a ta tedy spočívá na tom, kdo test plánuje nebo provádí. V tomto díle bychom chtěli detailněji probrat postup testování statistických hypotéz.
Rozdíl mezi popisnými a srovnávacími analýzami je zřejmý. U srovnávacích postupů existuje hypotéza nebo předpoklad, který měřením a následným testováním ověřujeme. Jde tedy primárně o analytický cíl, kdy srovnání provádíme například za účelem posouzení vlivu nějakého faktoru na zkoumané subjekty (tzv. vliv pokusného zásahu). Hypotézou pak rozumíme výrok (tvrzení), o jehož pravdivosti lze rozhodnout na základě analýzy dat jednoho nebo více náhodných výběrů. Dobře postavená hypotéza má při své neplatnosti jednoznačně definovanou alternativu vyjadřující opačnou skutečnost. Ve statistické terminologii hovoříme o tzv. nulové hypotéze (H0, null hypothesis), jelikož je standardní ji formulovat tak, aby její vyvrácení znamenalo důkaz existence podstatného (tedy „nenulového“) rozdílu. Je například formulována jako „mezi dvěma odhady průměru není rozdíl“, „celkové přežití pacientů se neprodlužuje“ nebo „parametry mezi sebou nesouvisí“. Nulová hypotéza tak může vyjadřovat opak záměru nebo přání badatele.
Pravdivost nebo nepravdivost hypotézy se ověřuje statistickým testem, jehož číselný výstup má známé rozdělení pravděpodobnosti při platnosti nulové hypotézy. Výsledek testu je číselným vyjádřením tzv. testové statistiky. Jednoduše řečeno, jde vždy o rovnici, jejíž číselný výsledek má definované rozdělení, a je známo, s jakou pravděpodobností mohou nastat různé hodnoty. Velmi pravděpodobné nebo běžné hodnoty potvrzují platnost nulové hypotézy, málo pravděpodobné až extrémní hodnoty do tohoto rozdělení nepatří a indikují neplatnost hypotézy.
Je‑li výsledkem statistického testu málo pravděpodobná hodnota testové statistiky (posuzujeme z jejího jako variantu méně pravděpodobnou než např. 5 % nebo 1 %), hovoříme o málo pravděpodobné platnosti nulové hypotézy a zamítáme ji. Přitom vždy musíme uvést pravděpodobnost, při které zamítnutí provádíme. Pravděpodobnost nastání dosaženého nebo číselně ještě extrémnějšího výsledku testu je hodnocena jako hladina významnosti pro zamítnutí H0 (označuje se jako p). Je‑li tedy p < 0,05 (standardně užívaná hranice 5 %), hypotézu zamítáme a hovoříme o statisticky významném výsledku (například: statisticky významný, tj. nenulový, korelační koeficient, statisticky významný rozdíl mezi rameny studie, apod.). Hladina významnosti p (p value) vyjadřuje pravděpodobnost, za které bychom dostali daný nebo extrémnější výsledek testu, kdyby nulová hypotéza platila. Čím nižší je hodnota p, tím nižší je pravděpodobnost platnosti nulové hypotézy.
Výše uvedeným textem jsme snad dostatečně naplnili povinnost uvést terminologii statistického testování. Jsme přesvědčeni, že všichni čtenáři se již s hodnotou p setkali a umí ji interpretovat. Způsob používání tohoto ukazatele v praxi ale často není správný a hodnotě p je někdy přisuzována bez nadsázky až magická síla. Jako by toto jediné číslo, klesne‑li pod hodnotu 0,05, rozhodovalo o platnosti celých vědeckých teorií nebo o existenci přírodních jevů. Nezřídka se setkáváme až s emocionálním vnímáním, kdy je nízká hodnota p považována za úspěch experimentu nebo badatelské činnosti. Nic takového ovšem není na místě. Opakujme z předchozího dílu seriálu, že žádný univerzální a všemocný statistický ukazatel neexistuje a statistická významnost musí být vždy doplněna nezávislým rozborem věcné významnosti výsledku.
Celý systém výpočtu testu pracuje jako číselný indikátor platnosti/neplatnosti nulové hypotézy, pravděpodobnostně vyjádřitelný právě hodnotou p. A jako každý indikátor může i tento dávat špatné výsledky, je‑li nesprávně používán. Pojďme se nyní podívat, co to znamená. Postavením hypotézy nad konkrétními daty přesahuje analýza popisný cíl a směřuje k posouzení pravdivosti daného tvrzení, a tedy k provedení závěru. Situaci komplikuje variabilita získaných dat, která může v nejhorším případě maskovat i skutečně podstatné rozdíly mezi skupinami subjektů. Rozhodnutí o přijetí/zamítnutí H0 je tedy pravděpodobnostní a u všech statistických testů je spojeno s dvěma typy chyb, které jsou mezinárodně jednotně označovány jako a (chyba I. druhu) a b (chyba II. druhu), obr. 1. Sama hodnota p tudíž nemůže být nekriticky přijímána, neboť máme nezanedbatelnou pravděpodobnost, že se v závěru testu mýlíme a deklarujeme opak skutečnosti.
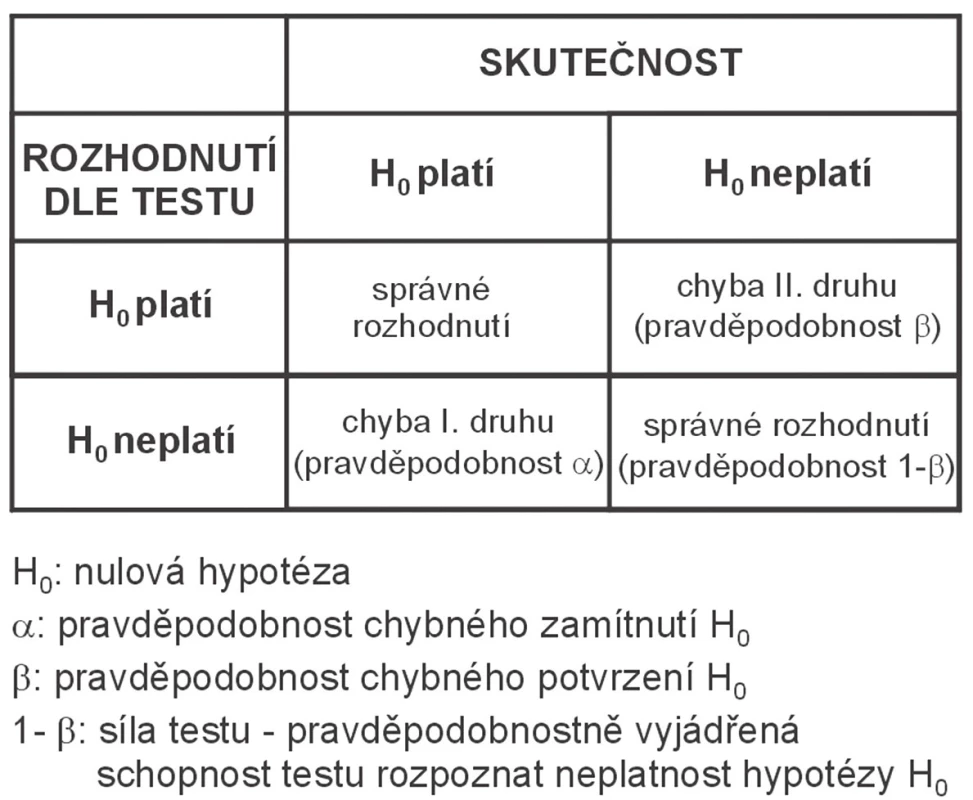
Rozborem chyb statistických testů se budeme detailně zabývat v dalším díle seriálu, nyní se zaměříme na jednoduchý popis celého procesu testování, neboť hočtenářům dlužíme. A možná nejen my. V současném světě můžeme provést i složité výpočty jednoduchým úderem do klávesy enter osobního počítače a podstata věci tak často mizí ze zřetele analytika a možnost chyby nabývá reálných rozměrů.
Jako příklad uvádíme srovnávání dvou výběrových odhadů průměru výšky lidské postavy v souborech A, B. Při srovnání budeme sledovat obecně platný postup uvedený na obr. 2:
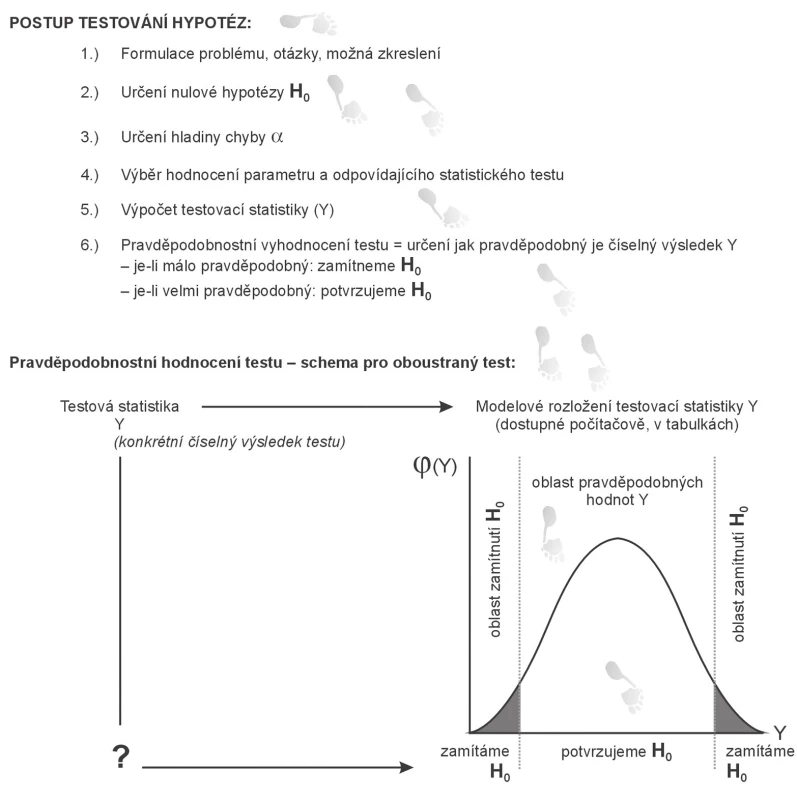
- Formulace problému je jasná: máme dva náhodné výběry osob (o velikosti nA, nB) a chceme srovnat jejich průměry. Výšku lidské postavy máme znalostně pod kontrolou, lehce posoudíme i reálný význam zjištěných rozdílů. Chceme srovnávat odhady průměrů, a data tak musí naplnit předpoklady normálního rozdělení, jinak by sám odhad průměru byl problematický.
- Nulová hypotéza H0: oba výběry se v průměrné výšce lidské postavy statisticky významně neliší. Zamítnutím H0 budeme tudíž prokazovat statisticky významný rozdíl. Tedy rozdíl, který není náhodný a převyšuje variabilitu znaku.
- Jako hladinu pravděpodobnosti chyby a zvolme paušálně používanou hladinu 0,05 (ačkoli to není rozhodně povinné – viz další díl seriálu). Tímto způsobem nastavujeme hraniční hodnotu p, a pokud dospějeme provedením testu k p < 0,05, budeme zamítat nulovou hypotézu na této hladině významnosti.
- Hodnocený znak, tedy výšku lidské postavy, vyjadřujeme jako aritmetický průměr. V tuto chvíli bez vysvětlení uvádíme, že pro srovnání dvou výběrových odhadů aritmetického průměru je používán tzv. t‑test, a to ve variantě pro dva nezávislé výběry (two‑sample t‑test).
- Výše uvedený postup je univerzální a vede k rovnici, jejímž výpočtem získáme testovou statistiku. V našem případě má Studentovo rozdělení (t) se stupni volnosti u = nA + nB – 2:
kde XA a XB jsou srovnávané aritmetické průměry, u kterých nulová hypotéza předpokládá rovnost, a s je vážená směrodatná odchylka obou výběrů, o které bylo pojednáno v minulém díle našeho seriálu. Váženou směrodatnou odchylku s lze s použitím směrodatných odchylek obou výběrů sA a sB vypočítat takto:
Dosazením a výpočtem výše uvedené rovnice získáme jedno číslo (hodnotu t), která má Studentovo rozdělení, pokud platí nulová hypotéza, tedy rovnost průměrů. Vyjde‑li nám t číselně malé (blízké nule), půjde o běžnou hodnotu a hypotéza zřejmě platí. Čím větší nebo menší t vyjde, tím je menší pravděpodobnost, že do daného rozdělení patří. A tím je menší pravděpodobnost, že hypotéza platí. V našem případě se tedy hodnota t chová jako výše zmíněný pravděpodobnostní indikátor platnosti nulové hypotézy.
Vyjde‑li hodnota t nepravděpodobně nízká nebo vysoká, nulovou hypotézu zamítneme. Jako hranici pro tento krok jsme zvolili hodnotu pravděpodobnosti 0,05, a tudíž pro zamítnutí hypotézy musí nastat tak vysoké t, že pouze 2,5 % všech hodnot může být vyšší (výsledek tedy musí přesáhnout kvantil t0,975 rozdělení statistiky t), anebo naopak tak nízké t, že jen 2,5 % hodnot je nižší než tento konkrétní výsledek (tedy níže než kvantil t0,025). Jak znázorňuje obr. 2, sledujeme obě strany rozdělení hodnot testové statistiky, neboť jsme při stanovení hypotézy určili rovnost průměrů a nepředjímáme, že jeden odhad bude větší než druhý. Logicky výše uvedený výpočet může vést k záporným i kladným hodnotám t. Takovou hypotézu označujeme jako oboustrannou (two‑tailed). Opakem je potom sledování jen jedné varianty (jednostranná hypotéza, one-tailed).
Až nyní dospěl náš výklad do bodu, kdy můžeme doložit, jak opatrně musíme při provádění testů postupovat a jak je nutné konkrétní výpočty kontrolovat. Tab. 1 uvádí čtyři příklady, které zde stručně komentujeme:
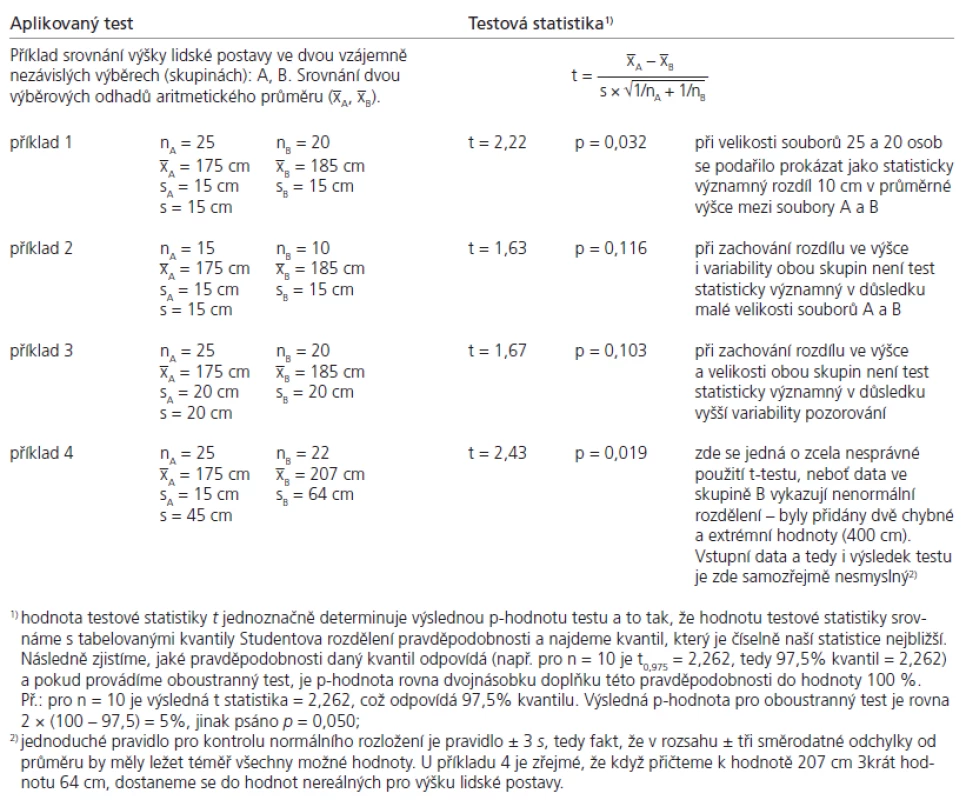
- Příklad 1 dokumentuje výpočet prokazující rozdíl 10 cm v průměrné výšce mezi soubory A a B jako statisticky významný (p = 0.032).
- Příklad 2 zahrnuje ten samý číselný rozdíl průměrů jako příklad 1, nicméně vzhledem k menší velikosti vzorku již neprokázaný jako statisticky významný (p = 0.116).
- Příklad 3 ukazuje rozdíl v průměrné výšce obou skupin lidí, který nebyl prokázán jako statisticky významný vzhledem k vyšší variabilitě měření (ve srovnání s příklady 1 a 2), stále ale při dodržení předpokladu normálního rozdělení.
- Příklad 4 dokumentuje zcela chybné použití tohoto statistického testu. K datům z příkladu 1 přibyly dvě nesmyslné extrémně odlehlé hodnoty, které mohou být překlepem datového managera (400 cm) a které zvýšily hodnotu pozorovaného rozdílu a směrodatné odchylky u skupiny B, což vedlo k statisticky významnému výsledku testu. Již samotné využití t‑testu je zde však špatné (!), neboť jeho základním předpokladem je právě normální rozdělení hodnot v obou srovnávaných výběrech. Jak vidno, samotný výpočet nemá žádnou kontrolní funkci a dospěje k výsledné hodnotě p, i když ta nemá reálný význam.
Poučení z číselného příkladu je jasné. Prostou změnou hodnot se mění číselný výstup testu a také jeho závěry včetně hodnoty p. Konkrétně zde uvedenou testovou statistiku t vedeme do vysokých nebo nízkých hodnot zvyšováním velikosti vzorku, snižováním variability měření a samozřejmě také zvětšováním rozdílu mezi průměry. Opačný vliv bude mít vyšší variabilita měření nebo vzájemné srovnávání menších výběrů.
Pokud jste dosud patřili mezi nekritické uživatele statistických testů, musíte být nyní na rozpacích. V tab. 1 zde dokládáme, že nejde o nic jiného než o výsledek jedné jediné rovnice, kterou lze nadto i zcela chybně použít. Dále je zřejmé, že změnou velikosti výběru (nA, nB) můžeme s výsledkem doslova manipulovat a prokazovat za statisticky významné velmi rozdílně hodnoty rozdílu x–A – x–B. Tento fakt dokládá i tab. 2, kde jsou propočítány výsledky výše uvedeného t‑testu pro různé n. Z toho samozřejmě nelze obviňovat rovnici samotnou, ta za nic nemůže. Když se do ní dosadí různá čísla, vyjde různě, to je její role v procesu. Odpovědným je výhradně experimentátor nebo analytik, ten musí vědět, co a proč do rovnice dosadil. Proces, kdy někdo svévolně mění například velikost vzorku, jen aby dosáhl statisticky významného výsledku (tab. 2), nelze označit za výzkum.

Závěrem lze formulovat následující jasná doporučení:
- Statistické testy ověřují platnost stanovených hypotéz na základě pravděpodobnostního hodnocení a může v nich dojít k chybám. Výsledky nelze přijímat nekriticky a bez kontroly.
- Statistické testy musí být vždy aplikovány s rozmyslem, neboť jsou založeny na konkrétních výpočtech a mají své předpoklady. Jejich ignorování vede k bezcennému výsledku.
- Aplikujeme‑li statistický test, měli bychom vždy vědět, co a proč testujeme, jaký rozdíl chceme zachytit jako statisticky významný, a také (!) jaký rozdíl skutečně můžeme zachytit jako významný (např. při dané velikosti výběru).
- Aplikace statistických testů retrospektivně na již náhodně nasbíraná data nemůže být považována za standardní situaci, neboť nemáme pod kontrolou základní komponenty, např. velikost vzorku. Zcela náhodně tedy pracujeme s příliš velkým nebo malým vzorkem, a výsledek testu je tedy také více méně náhodný. Pokud již musíme použít test v takové situaci, měli bychom to vždy podložit formulovanou hypotézou a dokladem, že získaná data takové testování umožňují (např. že velikost vzorku je dostatečná k průkazu reálně významného efektu – viz minulý díl seriálu).
- Standardní aplikace statistických testů zahrnuje plánovitou optimalizaci experimentu (sběru dat) a předcházející stanovení velikosti výběru nutné k prokázání potřebného efektu při dané variabilitě měření. Takový postup je povinný například u randomizovaných klinických studií fáze III. Za těchto okolností je výsledek statistického testu jednoznačně závazný a číselná hodnota p je průkazným indikátorem významnosti pozorovaných vlivů a změn.
Všechny tyto závěry budeme formou příkladů rozebírat v následujícím díle seriálu.
doc. RNDr. Ladislav Dušek, Dr.
Institut biostatistiky a analýz
Masarykova univerzita, Brno
e-mail: dusek@cba.muni.cz
Zdroje
1. Zar JH. Biostatistical methods. 2nd ed. London: Prentice Hall 1984.
2. Altman DG. Practical Statistics for Medical Research. London: Chapman and Hall 1991.
3. Riffenburgh RH. Statistics in Medicine. San Diego: Academic Press 1999.
4. Meinert CL. Clinical Trials: Design, Conduct and Analysis. Oxford: Oxford University Press 1996.
5. Shuster JJ. Handbook of sample size guidelines for clinical trials. London: CRC Press 1990.
Štítky
Dětská neurologie Neurochirurgie NeurologieČlánek vyšel v časopise
Česká a slovenská neurologie a neurochirurgie

2008 Číslo 6
-
Všechny články tohoto čísla
- Úvodní slovo
- Spánková apnoe dospělého věku
- Monitorování mozkové oxygenace
- Roztroušená skleróza mozkomíšní a magnetická rezonance: současnost a nové trendy
- Vztah atrofie amygdaly a dalších vybraných mozkových struktur k emocionální agnozii u Alzheimerovy nemoci
- Farmakoepidemiologická studie souboru 427 pacientů léčených pro epilepsii
- Rozdíly v počtu CAG opakování mezi pohlavími a jejich korelace s klinickým obrazem u Huntingtonovy choroby
- Vyšetřování proteinu 14-3-3 v mozkomíšním moku – klinicko‑patologická korelace
- Syndrom kubitálního kanálu. Srovnání operačních technik prosté dekomprese a přední transpozice ulnárního nervu
- Endonazální endoskopická transsfenoidální resekce selárních lézí
- Přední krční mikroforaminotomie v řešení unilaterální monosegmentální radikulopatie (prospektivně vedená pilotní studie – 15 pacientů)
- Extraoperativní mapování pomocí kortikálního gridu před resekcí difuzního oligodendrogliomu v řečově dominantní hemisféře – alternativa „awake kraniotomie“ – kazuistika
- Status absencí u geriatrického pacienta s recentní diagnózou idiopatické generalizované epilepsie – kazuistika
- Subakutně probíhající reverzibilní hypertenzní leukoencefalopatie – kazuistika
- Komentář ke článku Schreiberová et al. Sedace kombinací dexmedetomidin‑ketamin‑midazolam pro endovaskulární léčbu mozkových arteriovenózních malformací a stenóz karotických tepen
- Webové okénko
-
Analýza dat v neurologii
XII. Úvod do statistického usuzování – postupy a terminologie
- Česká a slovenská neurologie a neurochirurgie
- Archiv čísel
- Aktuální číslo
- Informace o časopisu
Nejčtenější v tomto čísle
- Roztroušená skleróza mozkomíšní a magnetická rezonance: současnost a nové trendy
- Spánková apnoe dospělého věku
- Subakutně probíhající reverzibilní hypertenzní leukoencefalopatie – kazuistika
- Vyšetřování proteinu 14-3-3 v mozkomíšním moku – klinicko‑patologická korelace


