Matematické modelování hemodynamiky mozkových aneuryzmat a možný přínos v klinické praxi z pohledu neurochirurga
Computational fluid dynamics of intracranial aneurysms and its potential contribution in clinical practice from a neurosurgeon’s perspective
Computational fluid dynamics have developed in the area of cerebrovascular diseases in recent years, especially in the research of intracranial aneurysms. The goal of most studies is to understand the pathophysiology of the initiation, growth and rupture of brain aneurysms and determine those risk hemodynamic parameters that lead to such processes. In our paper, we summarize the current state of art computational fluid dynamics especially from a surgical point of view of intracranial aneurysms and we focus on its possible contribution in clinical practice.
Key words:
aneurysm – computational fluid dynamics – wall shear stress Autoři deklarují, že v souvislosti s předmětem studie nemají žádné komerční zájmy.
The authors declare they have no potential conflicts of interest concerning drugs, products, or services used in the study.
The Editorial Board declares that the manuscript met the ICMJE “uniform requirements” for biomedical papers.
Autoři:
A. Hejčl 1,2; M. Stratilová 3; H. Švihlová 4; J. Hron 4; T. Radovnický 1; A. Sejkorová 1; A. Štekláčová 5; O. Bradáč 5; V. Beneš 5; M. Sameš 1; D. Dragomir-Daescu 6
Působiště autorů:
Neurochirurgická klinika UJEP, Krajská zdravotní, a. s., Masarykova nemocnice v Ústí nad Labem, o. z.
1; Mezinárodní centrum klinického výzkumu, FN u sv. Anny v Brně
2; 2. LF UK, Praha
3; Matematický ústav, MFF UK, Praha
4; Neurochirurgická a neuroonkologická klinika 1. LF UK, Praha
5; Department of Physiology & Biomedical Engineering, Mayo Clinic, Rochester, Minnesota, USA
6
Vyšlo v časopise:
Cesk Slov Neurol N 2018; 81(5): 532-538
Kategorie:
Přehledný referát
doi:
https://doi.org/10.14735/amcsnn2018532
Souhrn
V posledních letech se rozvinula metodika počítačového modelování toku tekutin v cerebrovaskulární problematice, především pak v oblasti intrakraniálních aneuryzmat. Cílem většiny studií je pochopit patofyziologii vzniku, růstu a ruptury mozkových výdutí a určit ty rizikové hemodynamické parametry, které k těmto procesům vedou. V naší práci shrnujeme současný stav počítačového modelování toku tekutin především z pohledu chirurgie mozkových aneuryzmat a zaměřujeme se na možný přínos pro klinickou praxi.
Klíčová slova:
aneuryzma – počítačové modelování tekutin – smykové napětí
Úvod
Nejčastější příčinou spontánní subarachnoidální hemoragie (SAH) je ruptura intrakraniální výdutě neboli aneuryzmatu. V ČR ošetříme ročně přibližně 700 mozkových výdutí, polovinu endovaskulárně a druhou polovinu chirurgicky. Z toho je 60 % prasklých aneuryzmat, které se projeví jako různě těžká forma SAH, a 40 % neprasklých výdutí řešených preventivně. Prevalence neprasklých intrakraniálnich aneuryzmat v dospělé populaci je asi 3 % [1,2] a pouze malé procento z nich praskne [3]. Rozvoj a rozšíření neurozobrazovacích metod vede k jejich zvýšenému záchytu. Zatímco v roce 1998 byl na Neurochirurgické klinice v Ústí nad Labem podíl ošetřených neprasklých aneuryzmat na celkovém počtu 20 %, v posledních několika letech se podíl ošetřených neprasklých aneuryzmat pohybuje okolo 50 %. Proto je problematika indikací ošetření neprasklých intrakraniálních aneuryzmat stále aktuálnější. Jedná se o preventivní výkon s rizikem komplikací, které se dle různých studií pohybuje v rozmezí 7,7 – 28,9 % [4,5] a mortalitou 0 – 3,2 % [5]. Na druhou stranu je ruptura aneuryzmatu spojená s vysokou morbiditou a mortalitou. Ve vyspělých zemích (Japonsko, USA, Evropa) je riziko úmrtí pacientů, kteří se dostanou do nemocnice 27 – 44 % [6]. K tomu dalších 12 – 15 % jedinců zemře ještě před převozem do zdravotnického zařízení. Důležitý je proto správný výběr pacientů k preventivnímu ošetření na základě hodnocení rizikových faktorů ruptury. Při znalosti rizika ošetření mozkové výdutě na daném pracovišti by pak bylo možno relativně jednoduše nabídnout nejlepší možné řešení – pokud bude riziko ošetření vyšší, je lepší pouhá observace, v opačném případě pak můžeme doporučit aktivní ošetření aneuryzmatu [7].
Přirozené riziko ruptury mozkového aneuryzmatu je samozřejmě multifaktoriální. Mezi hlavní faktory patří velikost aneuryzmatu, jeho morfologie a lokalizace, dále anamnéza předchozí SAH, arteriální hypertenze, kouření a pohlaví. Mezinárodní tým autorů se snažil kvantifikovat vliv jednotlivých rizikových faktorů po zohlednění šesti nejvýznamnějších studií zabývajících se neprasklými intrakraniálními aneuryzmaty [8]. Vyvinuli tzv. skóre PHASES, které převádí výše uvedené rizikové faktory do kvantifikační škály. Název PHASES je souhrnem počátečních písmen šesti hlavních rizikových faktorů – etnikum (P – population), hypertenze (H – hypertension), věk (A – age), velikost aneuryzmatu (S – size), anamnéza SAH z jiného aneuryzmatu (E – earlier subarachnoid hemmorhage from another aneurysm) a lokalizace aneuryzmatu (S – site of aneurysm). Výsledné skóre (od nejmenší hodnoty < 2 po nejvyšší > 12) se pak převádí na 5leté riziko ruptury. O rok později publikoval tým 69 autorů ještě komplexnější skórovací systém (The Unruptured Intracranial Aneurysm Treatment Score; UIATS). Výsledkem je relativně hrubá kvantifikace poměru mezi přirozeným rizikem a rizikem intervence [9].
Veškerá skórovací schémata jsou založena na hodnocení rizikových faktorů ruptury získaných z rozsáhlých statistických studií. Nicméně v patofyziologii ruptury mozkových aneuryzmat hraje zásadní roli poměr mezi kvalitou cévní stěny a parametry toku krve (hemodynamika). Právě výše uvedené rizikové faktory (kouření, arteriální hypertenze, věk) ovlivňují jak kvalitu stěny cévy, tak i hemodynamiku. Zatímco hodnocení kvality stěny cévy neinvazivně je v samých počátcích, kvantifikace parametrů hemodynamiky je dnes již možná. Matematické modelování hemodynamiky (computational fluid dynamics; CFD) je progresivně se rozvíjející mezioborový směr, jehož výsledky se v některých případech mohou zúročit v klinické praxi [10]. Cílem naší práce je podat krátký souhrn současného stavu modelování hemodynamiky v problematice mozkových aneuryzmat z pohledu neurochirurga s důrazem na možné uplatnění výsledků výzkumu v klinické praxi.
Matematické modelování hemodynamiky
Vlastní proces modelování hemodynamických parametrů se skládá z několika kroků. Vytvoření 3D modelu se děje pomocí manuální či automatické segmentace. Jako zdrojová data se využívají angiografická vyšetření (3D angiografie, CTA či MRA). Každá z metod má své limitace (kalcifikace, tokové artefakty apod.) Několik studií se snažilo posoudit vztah mezi různými zobrazovacími vyšetřeními [11,12]. V jedné takové studii porovnávali autoři výsledky CFD získané při segmentaci z CTA či digitální subtrakční angiografie (DSA) [11]. V závěru autoři konstatují, že i přes kvantitativní rozdíly v jednotlivých parametrech hemodynamiky mezi CTA a DSA segmentovanou skupinou byly základní charakteristiky toku u obou skupin shodné.
V dalším kroku je na takto vytvořeném geometrickém modelu proveden výpočet s pomocí Navier-Stokesových rovnic, jež popisují proudění nestlačitelné vazké tekutiny. Použití numerického řešení Navierových-t rovnic v sobě obsahuje také předpoklad laminárního proudění. Jsou zkoumány možné vlivy jevů, které nejsou tímto modelem zachyceny, např. vliv turbulentního proudění nebo vliv změny viskozity v závislosti na rychlosti smyku [13].
Tyto výpočty charakterizují proudění, tj. podávají kompletní informaci o rychlosti tekutiny a tlaku na cévní stěnu a o veličinách z nich odvozených jako např. tenzor napětí. Díky neurčitosti v popisu oblasti a také zadaných okrajových podmínkách může být variabilita těchto veličin významná, avšak určité globální odvozené veličiny – smykové napětí (wall shear stress; WSS) a oscilační smykový index (oscillatory shear index; OSI) se shodují pro určitou variaci v přesnosti numerických řešení [14]. WSS je definováno jako tlak, který působí paralelně s lumen cévy, krevním tokem. OSI pak popisuje rozdíl mezi vektorem WSS a tokem krve v průběhu srdečního cyklu.
Vývoj intrakraniálního aneuryzmatu můžeme rozdělit na tři fáze – iniciaci, růst a stabilizaci. Jen malé procento aneuryzmat je nestabilních, progreduje a nakonec skončí rupturou. Právě růst, změna tvaru a ruptura aneuryzmatu jsou ty situace, které se snažíme pomocí matematického modelování pochopit a odhadnout riziko vzniku těchto kritických fází vývoje.
Hemodynamika a vznik mozkových aneuryzmat
Vznik výdutě je způsoben nepoměrem mezi tahovým napětím ve stěně cévy a hemodynamickými inzulty, kterým je stěna vystavena. Tlakové napětí ovlivňuje obrat, syntézu a rozpad kolagenu uvnitř cévní stěny. Intrakraniální cévy jsou charakteristické malým průměrem s vysokým krevním průtokem. Proto jsou ovlivněny WSS krevních částic působících na jejich stěnu. WSS je detekováno endoteliálními buňkami, které tyto mechanické signály transformují na biologické a tím zajištují homeostázu a remodelaci stěny cév [15]. Patologické hodnoty WSS pak navozují změny ve stěnách přenášené endoteliálními buňkami, jako jsou prozánětlivé reakce, aktivace metaloproteináz, degradace extraceluárního matrixu, destrukční remodelace či úmrtí buněk. Tlakové napětí vyvolá tahové napětí v cévní stěně, na které reagují hladké svalové buňky, fibroblasty a myofibroblasty regulující dynamiku kolagenu [16,17]. Právě v bifurkaci intrakraniálních cév je WSS nejvyšší, což přispívá k rozvoji aneuryzmat [18].
Geometrie cévní stěny neustále ovlivňuje charakter toku a jeho parametry. Větvení cév na bázi mozku na Willisově okruhu generuje v bifurkacích cév komplexní charakter toku s vysokým WSS, což vede k remodelaci cévní stěny a potenciálně vzniku mozkového aneuryzmatu [19,20]. Vysoké WSS nejspíše spouští kaskádu na buněčné úrovni, která vede k histologickým změnám cévní stěny s následným oslabením. Navíc anatomické variace cév na bázi mozku (změna velikosti cév, úhlů mezi cévami, ageneze cév, např. karotid apod.) vedou k dalším atypiím v hemodynamice a zvýšení rizika vzniku mozkového aneuryzmatu. Sami jsme z klinické praxe takový příklad raritně uloženého aneuryzmatu na junkci zadní mozkové tepny (P12) a zadní spojovací tepny (PCom) u pacienta s uzávěrem obou karotických tepen popsali [21].
Dalším patofyziologickým mechanizmem vzniku aneuryzmatu je vliv WSS na sekreci faktorů z endoteliálních buněk, jako jsou oxid dusnatý (NO), prostaglandiny nebo endoteliální růstové faktory. Tyto pak vedou ke změně cévního napětí či remodelaci cévní stěny. V oblastech s nízkým WSS, tedy v zónách, kde stagnuje krevní tok, dochází k adhezi leukocytů pomocí adhezivních molekul, jako je vascular adhesion molecule-1 (VAM-1). Adheze leukocytů pak může vést k aktivací imunitních a zánětlivých změn, které nabourávají stávající strukturu cévní stěny a mohou vést k jejímu zeslabení. Tlakové působení na cévní stěnu vede k lokální dilataci a tím iniciaci mozkového aneuryzmatu. Naopak vysoké WSS vede ke zvýšení koncentrace NO a inhibici proliferace hladkých svalových buněk v cévní stěně. Na druhou stranu cévní stěna může být oslabená rozličnými získanými (arteriální hypertenze, kouření) nebo geneticky danými faktory. Existují některá hereditární onemocnění, se kterými je spojován vyšší výskyt mozkových výdutí jako autozomálně dominantní polycystóza ledvin, Ehler-Danlosův syndrom typ IV nebo fibromuskulární dysplázie. Tato onemocnění snižují práh pro patologickou odpověď cévní stěny na hemodynamický inzult [16,17].
Bočná (nástěnná) aneuryzmata jsou určitou specifickou podskupinou intrakraniálních aneuryzmat. Mantha et al provedli studii, ve které porovnali WSS právě u pacientů s bočnými aneuryzmaty a cévou upravenou virtuálním odstraněním aneuryzmatu [22]. Tato studie ukázala, že WSS je v místě vzniku budoucího aneuryzmatu nízké, což je nejspíše dáno stagnací krevního toku.
Hemodynamika a růst mozkových aneuryzmat
Vznik aneuryzmatu je následován buď jeho stabilizací, nebo dalším růstem s rizikem ruptury. Roční riziko růstu je u 3 – 6 % všech aneuryzmat [4,11,12] a 2,6 – 4,5 % všech malých aneuryzmat [4,7,12] (obr. 1A, B). Růst aneuryzmatu je známkou jeho instability a vyššího rizika ruptury. Proto je tendence takováto aneuryzmata preventivně ošetřit. Aneuryzmata mohou růst buď jako celek, nebo může dojít jen k růstu v určité malé oblasti (fokální růst) s rozvojem tzv. blebu či sekundárního aneuryzmatu. Několik studií ukázalo, že globální růst probíhá spíše v oblastech nízkého WSS a vysokého OSI [23] (obr. 1C). Na druhou stranu oblasti vysokého WSS s velkým gradientem WSS způsobují remodelaci v oblasti krčku aneuryzmatu [2,24,25]. Machi et al posuzovali vztah mezi WSS a typem růstu. U aneuryzmat s fokálním růstem bylo v místě růstu WSS nízké WSS s vysokým OSI, zatímco u aneuryzmat s globálním růstem bylo WSS vysoké s vysokým prostorovým gradientem WSS [26]. Nicméně zásadním faktorem je dynamika v čase. Cebral et al zjistili, že rozvoj sekundárních váčků („blebs”) probíhá v místech s vysokým WSS a po jejich formaci dojde k jeho snížení [25]. Bude třeba dalších studií s větším počtem aneuryzmat. Dosud největší studie zabývající se hemodynamikou a růstem byla založena na hodnocení „pouhých” 27 aneuryzmat [27].
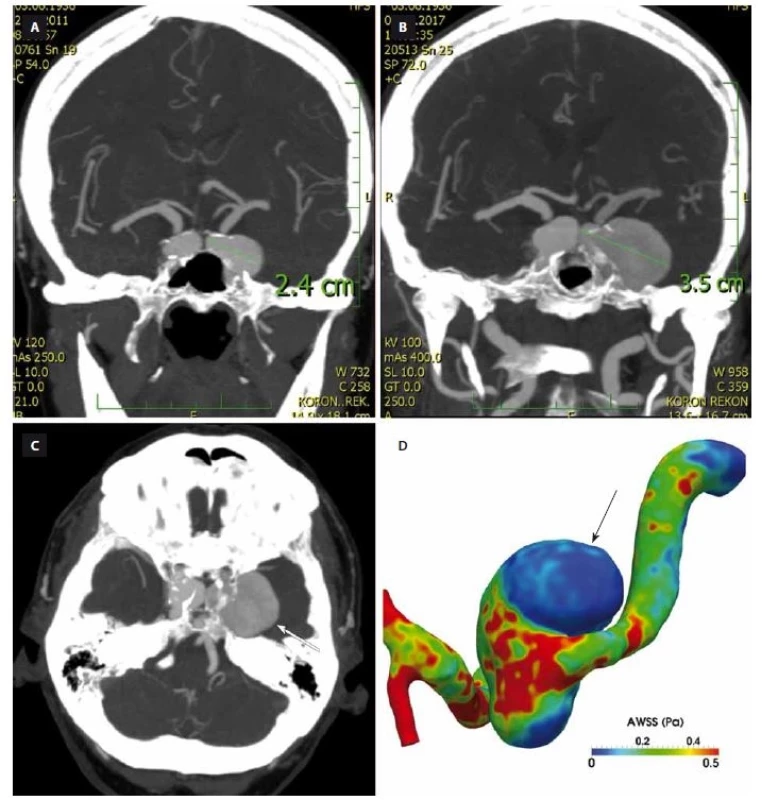
A – CTA z roku 2011 zobrazuje bilaterální karotická aneuryzmata v segmentu kavernózního splavu.
B – CTA z roku 2017 prokazuje růst obou aneuryzmat, vlevo je již aneuryzma gigantické, v max. rozměru dosahuje 35 mm.
C – CTA u stejné pacientky ukazuje, jak je růst kavernózních aneuryzmat ovlivněn okolními kostními strukturami báze lební (šipka ukazuje
místo růstu aneuryzmatu).
D – Hemodynamické parametry kalkulované u gigantického aneuryzmatu kavernózního splavu vlevo ukazují, že místa růstu jsou v oblastech
s nízkým smykovým napětím (šipka).
Fig 1. Growth of intracranial aneurysm and computational fluid dynamics analysis. AWSS – average wall shear stress
A – CTA from 2011 shows bilateral carotid aneurysms in cavernous segment.
B – CTA from 2017 shows growth of both aneurysms, where the left-sided one is already giant with a max. diameter of 35 mm.
C – CTA of the same patient shows how the growth of the left cavernous aneurysms is infl uenced by surrounding bony structures of the
skull base (arrow shows the expanding part of the aneurysm).
D – Hemodynamic parameters in a giant aneurysm of the left cavernous segment show that the area of growth is correlated with low wall
shear stress (arrow).
Existuje několik studií, které hodnotí vliv WSS na růst aneuryzmatu s různými výsledky. Meng et al navrhli koncept, ve kterém jak vysoké, tak nízké WSS hrají úlohu v růstu a ruptuře aneuryzmat, přičemž se liší v mechanizmu působení [16]. Dle tohoto konceptu vysoké WSS vede spíš k aktivaci hladkých svalových buněk a fibroblastů (mural-cell mediated pathway), zatímco nízké WSS vede k aktivaci zánětlivých buněk (inflammatory-cell mediated pathway). Proti tomuto konceptu však jde jedna z prvních studií korelujících hemodynamické modelace s histologií; v této byl zánět asociován s vyšším tokem vč. zvýšeného WSS [28].
Růst aneuryzmatu je ovlivněn nejen vnitřními faktory, ale také okolním prostředím, které může významně ovlivnit jeho tvar a růst. Příkladem jsou kostní struktury baze lební u aneuryzmat vnitřní karotidy či bazilární tepny apod. [26] (obr. 1D).
Hemodynamika ve vztahu k riziku ruptury aneuryzmatu
Degenerace stěny aneuryzmatu postupuje od krčku směrem ke kopuli vaku. Ruptura aneuryzmatu většinou nastane v místě apexu, což je také často oblast nízkého WSS. Tvar vaku ovlivňuje charakter toku a tím i jeho jednotlivé vlastnosti. Uvnitř aneuryzmat s úzkým krčkem může být pomalý tok s recirkulacemi, což se projeví nízkým WSS vedoucím ke zvýšené degeneraci cévní stěny.
Hemodynamické změny uvnitř aneuryzmatu jsou přenášeny biologickými signály dovnitř cévní stěny a vedou tak k jejím mikroskopickým změnám [29]. NO je klíčový mediátor nízkého WSS a oscilací ve WSS. Nízké WSS dále podporuje expresi adhezivních molekul, jako je VCAM-1 a ICAM-1.
Velké množství studií se zaměřilo na rozdíly v hemodynamických parametrech mezi prasklými a neprasklými aneuryzmaty. Zhou et al provedli metaanalýzu 22 studií čítající 1 257 jedinců a zjistili, že právě nízké WSS (0 – 1,5 Pa) ve vaku aneuryzmatu je charakteristické pro prasklá aneuryzmata [30]. Předpokládá se, že WSS o velikosti přibližně 2,0 Pa (N/ m2) je z hlediska zachování cévní stěny stěny nejvhodnější. WSS nižší než 1,5 Pa vede k apoptóze endoteliálních buněk [31]. Například Takao et al zjistili, že minimální hodnota WSS u prasklých aneuryzmat byla poloviční v porovnání s neprasklými aneuryzmaty. Nízké WSS tak může být indikátorem zvýšeného rizika ruptury intrakraniálního aneuryzmatu. Dále několik autorů prokázalo, že u prasklých aneuryzmat je oblast nízkého WSS v porovnání s neprasklými aneuryzmaty větší [32 – 34]. Na druhou stranu Cebral et al porovnali výsledky CFD u 210 aneuryzmat a zjištění v jejich studii ukázala, že prasklá aneuryzmata mají koncentrovaný proud krve a vyšší WSS s vyšší maximální hladinou WSS.
Nemalé množství studií provedlo hodnocení hemodynamiky u prasklých mozkových výdutí, u kterých bylo identifikováno místo ruptury [35 – 37]. V převážné většině se jednalo o chirurgické série, kdy neurochirurg identifikoval místo ruptury perioperačně (obr. 2A). Existují také výjimečné kazuistiky endovaskulární, kdy dojde k ruptuře periprocedurálně přímo na angiolince [38]. Po vytvoření 3D sítě jsou následně kalkulovány hemodynamické parametry v aneuryzmatu se zaměřením na místo ruptury (obr. 2B). Toto je často charakterizováno specifickými hodnotami hemodynamických parametrů. Dle několika studií je oblast prasknutí v místě přímého trysku krve směrem proti stěně aneuryzmatu [36,38,39] (obr. 2C). Taková situace byla popsána též u aneuryzmatu terminální bazilární tepny několik hodin před jeho prasknutím [40]. Pokud se týká WSS a místa ruptury, výsledky jsou zatím rozličné. Zatímco někteří autoři ukazují, že místo ruptury je v oblasti s nízkým WSS [35,37] (obr. 2D), tak jiné práce, vč. naší, dokumentují místo ruptury v okrsku vysokého WSS [36,38].
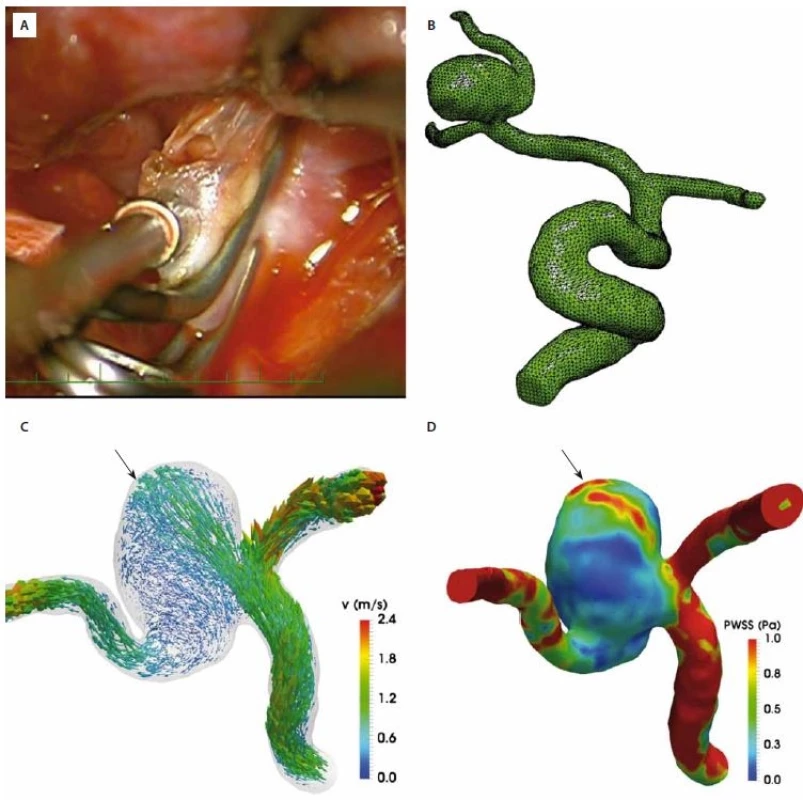
A – Aneuryzma M12 vpravo po naložení dvou zahnutých klipů Aesculap se zobrazeným místem ruptury.
B – Výsledná 3D síť, která sloužila jako morfologický základ intrakraniálních tepen a aneuryzmatu ke kalkuaci hemodynamických parametrů
.
C – Rychlostní křivky zobrazují dominantní směr toku a jeho charakter. Místo ruptury zde koreluje s vtokovým tryskem krve z segmentu M1
arteria cerebri media.
D – Mapa WSS. Místo ruptury opět koreluje s oblastí zvýšeného WSS.
Fig 2. Computational fl uid dynamics in a patient with a ruptured right middle cerebral artery bifurcation (M12) aneurysm treated with
a clip and a perioperatively identifi ed site of rupture. WSS – wall shear stress; PWSS – peak WSS
A – Right M12 aneurysm after applying two curved Aesculap clips with a perioperatively identifi ed site of rupture.
B – The 3D mesh of the intracranial blood vessels and the aneurysm used for calculating hemodynamic parameters.
C – Velocity curves showing the dominant direction of flow and its characteristics. The site of rupture is correlated with a jet flow from the
M1 segment of the middle cerebral artery.
D – The map of the WSS. The site of rupture is correlated with an area of WSS.
Jedním z nedostatků matematického modelování je zatím malé množství studií, které by korelovaly vztah mezi biologií cévní stěny a hemodynamikou. Přitom nalézt vztah mezi histologickými změnami a hemodynamickými parametry by mohlo zpřesnit její výpovědní hodnotu a tím posunout tuto metodu blíže k reálnému využití. Frösen et al klasifikovali čtyři typy histologické stavby stěn aneuryzmat na základě poškození struktury cévní stěny, myointimálni hyperplázie, proliferace hladkých svalových buněk a přítomnosti organizovaného trombu [41]. Stěna prasklého aneuryzmatu je častěji charakterizována tím, že je dezorganizovaná, tenčí, hypocelulární a je přítomen organizovaný trombus. Jednotlivé typy stavby cévní stěny v rámci jedné výdutě mohou přecházet jedna v druhou. Jedna z prvních studií, která se snaží korelovat hemodynamické parametry s charakterem cévní stěny, byla publikována nedávno [28]. Autoři celkem překvapivě vzhledem k původním předpokladům zjistili, že vysoké WSS a vysokorychlostní charakter toku souvisely s nálezem zánětlivých změn ve stěně aneuryzmatického vaku, zatímco oblasti nízkého toku souvisely s degenerativními změnami ve stěně aneuryzmatu a ztrátou buněk hladkého svalu a pericytů. Korelace histologických změn a hemodynamiky se přitom vyhýbá riziku chyby při porovnání prasklých a neprasklých aneuryzmat. Pravděpodobně bude rozdíl mezi aneuryzmatem, které nepraskne nikdy, a mezi aneuryzmatem, jehož ruptura je otázkou času. Jaké aneuryzma právě analyzujeme, nevíme.
Nevýhodou hodnocení hemodynamických parametrů u prasklých mozkových výdutí je fakt, že se většinou hodnotí parametry hemodynamiky u aneuryzmat po ruptuře. Vlastní morfologie vaku přitom může být změněna proti stavu před rupturou, a proto získané výsledky nemusí být pro předpověď rizika ruptury zcela relevantní [42]. V naší vlastní práci jsme zjistili, že ve vývoji aneuryzmatu, u kterého nastala ve finále ruptura, došlo k vzniku sekundárního vaku, častého místa ruptury [43]. V tomto místě došlo ke snížení WSS a zpomalení toku.
Matematické modelování hemodynamiky z pohledu neurochirurga
Modelace a hodnocení hemodynamických parametrů rozšiřuje náš pohled na mozková aneuryzmata. Tuto metodiku rozvíjeli převážně endovaskulární radiologové s cílem posoudit vliv endovaskulární terapie, např. stentů či flow-diverterů, na léčbu a vývoj aneuryzmatu po implantaci. Nicméně narůstající záchyt neprasklých aneuryzmat vede k nutnosti zpřesnění a nejlépe individuálního stanovení rizika ruptury. Tuto metodiku tak mohou využít i neurochirurgové jak při sledování aneuryzmatu, tak i indikaci k léčbě [43]. Některé aspekty v souvislosti s rozvojem problematiky matematického modelování lze navíc získat jen při neurochirurgických operacích – přímá vizualizace stěny aneuryzmatu pod mikroskopem (kalcifikace, zeslabení stěny, trombóza), identifikace místa ruptury, odběr stěny výdutě k histologickému vyšetření po jejím zaklipování apod. Perioperační nález lze pak verifikovat histologickým vyšetřením a toto korelovat s výsledky hemodynamických parametrů, což může v konečném důsledku vést k lepší korelaci mezi matematickými modely a biologickými vlastnostmi stěny cév a mozkových výdutí. Některé takové studie se již objevují [28].
Z klinického hlediska je zásadní, aby parametry hemodynamiky byly využitelné v klinické praxi. Existuje např. studie poukazující na vztah mezi hemodynamikou a rizikem selhání endovaskulární léčby ošetřeného aneuryzmatu na hrotu bazilární tepny [44]. Konkrétními parametry, které jsou nejčastěji zmiňovány s možným brzkým klinických využitím, jsou WSS a charakter toku. Velké množství studií ukazuje, že aneuryzmata s nízkým WSS a komplexním tokem jsou spojena s vyšším rizikem ruptury [30,45]. Další vývoj CFD v problematice intrakraniálních aneuryzmat tak může přinést užitečné informace ve stále aktuálnějším tématu. Na druhou stranu je nutno konstatovat, že velké množství studií CFD u mozkových aneuryzmat prezentuje často rozdílné či rozporuplné výsledky. Jedním z důvodů může být rozličná metodika různých výzkumných skupin, jak se projevilo v mezinárodní studii CFD Rupture Challenge [46,47]. Do budoucnosti je proto nutné, aby se metodika matematického modelování postupně sjednotila tak, aby bylo možno výsledky porovnat celosvětově.
Další nevýhodou CFD modelace je relativně složitý protokol s nutností zahrnout náročné kalkulace s využitím často superpočítačových clusterů. Nicméně díky technologickému vývoji se již objevují studie, které ukazují, že parametry hemodynamiky lze popsat v rámci vyšetření pacienta na MR, čili modalitě často užívané vzhledem k absenci radiační zátěže k longitudinálnímu sledování neprasklých aneuryzmat [48]. Můžeme očekávat, že další technologický vývoj nabídne zhodnocení hemodynamických parametrů v rámci standardního algoritmu MR vyšetření. V takovém případě můžeme kvantifikovat riziko jak v rámci vstupního vyšetření, tak i jeho vývoj v čase při opakovaných MR vyšetřeních.
Závěr
Matematické modelování se v problematice intrakraniálních aneuryzmat v posledních letech rozvíjí. Rozšiřuje naše poznání týkající se patofyziologie jejich vzniku, vývoje a ruptury. I přes zřejmé limitace této metody se ukazují některé rozdíly v hemodynamice, např. mezi prasklými a neprasklými aneuryzmaty. Recentní studie pak propojují biologii cévní stěny s hemodynamickými parametry, což může vývoj významně posunout. Další posun lze též očekávat od technologického pokroku, který může průběh matematického modelování zrychlit a zjednodušit. V blízké budoucnosti tak nejspíše zjistíme, zda tato metodika dosáhne reálného využití v klinické praxi či nikoli.
Práce byla podpořena grantem AZV 17-32872A.
Výpočetní část této práce byla podpořena MŠMT z OP VaVpI Centrum excelence IT4 Innovations (IT4I) – LM2015070.
Autoři deklarují, že v souvislosti s předmětem studie nemají žádné komerční zájmy.
Redakční rada potvrzuje, že rukopis práce splnil ICMJE kritéria pro publikace zasílané do biomedicínských časopisů.
MUDr. Aleš Hejčl, Ph.D.
Neurochirurgická klinika UJEP
Krajská zdravotní, a. s.
Masarykova nemocnice v Ústí nad Labem, o. z.
Sociální péče 3316 /12A
401 13 Ústí nad Labem
e-mail: ales.hejcl@gmail.com
Přijato k recenzi: 26. 5. 2018
Přijato do tisku: 19. 7. 2018
Zdroje
1. Vlak MH, Algra A, Brandenburg R et al. Prevalence of unruptured intracranial aneurysms, with emphasis on sex, age, comorbidity, country, and time period: a systematic review and meta-analysis. Lancet Neurol 2011; 10(7): 626 – 636. doi: 10.1016/ S1474-4422(11)70109-0.
2. Sugiyama S, Meng H, Funamoto K et al. Hemodynamic analysis of growing intracranial aneurysms arising from a posterior inferior cerebellar artery. World Neurosurg 2012; 78(5): 462 – 468. doi: 10.1016/ j.wneu.2011.09.023.
3. Rinkel GJ, Djibuti M, Algra A et al. Prevalence and risk of rupture of intracranial aneurysms: a systematic review. Stroke 1998; 29(1): 251 – 256.
4. Nanda A, Patra DP, Bir SC et al. Microsurgical clipping of unruptured intracranial aneurysms: a single surgeon‘s experience over 16 Years. World Neurosurg 2017; 100 : 85 – 99. doi: 10.1016/ j.wneu.2016.12.099.
5. Kerezoudis P, McCutcheon BA, Murphy M et al. Pre-dictors of 30-day perioperative morbidity and mortality of unruptured intracranial aneurysm surgery. Clin Neurol Neurosurg 2016; 149 : 75 – 80. doi: 10.1016/ j.clineuro.2016.07.027.
6. Connolly ES Jr., Rabinstein AA, Carhuapoma JR et al. Guidelines for the management of aneurysmal subarachnoid hemorrhage: a guideline for healthcare professionals from the American Heart Association/ american Stroke Association. Stroke 2012; 43(6): 1711 – 1737. doi: 10.1161/ STR.0b013e3182587839.
7. Molyneux A, Kerr R, Stratton I et al. International Subarachnoid Aneurysm Trial (ISAT) of neurosurgical clipping versus endovascular coiling in 2143 patients with ruptured intracranial aneurysms: a randomised trial. Lancet 2002; 360(9342): 1267 – 1274.
8. Greving JP, Wermer MJ, Brown RD et al. Development of the PHASES score for prediction of risk of rupture of intracranial aneurysms: a pooled analysis of six prospective cohort studies. Lancet Neurol 2014; 13(1): 59 – 66.
9. Etminan N, Brown RD Jr., Beseoglu K et al. The unruptured intracranial aneurysm treatment score: a multidisciplinary consensus. Neurology 2015; 85(10): 881 – 889. doi: 10.1212/ WNL.0000000000001891.
10. Caroff J, Mihalea C, Da Ros V et al. A computational fluid dynamics (CFD) study of WEB-treated aneurysms: Can CFD predict WEB „compression“ during follow-up? J Neuroradiol 2017; 44(4): 262 – 268. doi: 10.1016/ j.neurad.2017.03.005.
11. Geers AJ, Larrabide I, Radaelli AG et al. Patient-specific computational hemodynamics of intracranial aneurysms from 3D rotational angiography and CT angiography: an in vivo reproducibility study. AJNR Am J Neuroradiol 2011; 32(3): 581 – 586. doi: 10.3174/ ajnr.A2306.
12. Ren Y, Chen GZ, Liu Z et al. Reproducibility of image-based computational models of intracranial aneurysm: a comparison between 3D rotational angiography, CT angiography and MR angiography. Biomed Eng Online 2016; 15(1): 50. doi: 10.1186/ s12938-016-0163-4.
13. Evju O. On the assumption of laminar flow in physiological flows: cerebral aneurysms as an illustrative example, modeling the heart and the circulatory system. In: Quarteroni A (ed). Modeling the heart and the circulatory system. Basel: Springer International Publishing 2015 : 177 – 195.
14. Evju O, Pozo JM, Frangi AF et al. Robustness of common hemodynamic indicators with respect to numerical resolution in 38 middle cerebral artery aneurysms. PLoS One 2017; 12(6): e0177566. doi: 10.1371/ journal.pone.0177566.
15. Nixon AM, Gunel M, Sumpio BE. The critical role of hemodynamics in the development of cerebral vascular disease. J Neurosurg 2010; 112(6): 1240 – 1253. doi: 10.3171/ 2009.10.JNS09759.
16. Meng H, Tutino VM, Xiang J et al. High WSS or low WSS? Complex interactions of hemodynamics with intracranial aneurysm initiation, growth, and rupture: toward a unifying hypothesis. AJNR Am J Neuroradiol 2014; 35(7): 1254 – 1262. doi: 10.3174/ ajnr.A3558.
17. Frosen J, Tulamo R, Paetau A et al. Saccular intracranial aneurysm: pathology and mechanisms. Acta Neuropathol 2012; 123(6): 773 – 786. doi: 10.1007/ s00401-011-0939-3.
18. Rossitti S, Lofgren J. Optimality principles and flow orderliness at the branching points of cerebral arteries. Stroke 1993; 24(7): 1029 – 1032.
19. Geers AJ, Morales HG, Larrabide I et al. Wall shear stress at the initiation site of cerebral aneurysms. Biomech Model Mechanobiol 2017; 16(1): 97 – 115. doi: 10.1007/ s10237-016-0804-3.
20. Valen-Sendstad K, Piccinelli M, Steinman DA. High-resolution computational fluid dynamics detects flow instabilities in the carotid siphon: implications for aneurysm initiation and rupture? J Biomech 2014; 47(12): 3210 – 3216. doi: 10.1016/ j.jbiomech.2014.04.018.
21. Orlicky M, Sames M, Hejcl A et al. Carotid-ophthalmic aneurysms: Our results and treatment strategy. Br J Neurosurg 2015; 29(2): 237 – 242. doi: 10.3109/ 02688 697.2014.976176.
22. Mantha A, Karmonik C, Benndorf G et al. Hemodynamics in a cerebral artery before and after the formation of an aneurysm. AJNR Am J Neuroradiol 2006; 27(5): 1113 – 1118.
23. Boussel L, Rayz V, McCulloch C et al. Aneurysm growth occurs at region of low wall shear stress: patient-specific correlation of hemodynamics and growth in a longitudinal study. Stroke 2008; 39(11): 2997 – 3002. doi: 10.1161/ STROKEAHA.108.521617.
24. Meng H, Metaxa E, Gao L et al. Progressive aneurysm development following hemodynamic insult. J Neurosurg 2011; 114(4): 1095 – 1103. doi: 10.3171/ 2010.9.JNS10368.
25. Cebral JR, Sheridan M, Putman CM. Hemodynamics and bleb formation in intracranial aneurysms. AJNR Am J Neuroradiol 2010; 31(2): 304 – 310. doi: 10.3174/ ajnr.A1819.
26. Machi P, Ouared R, Brina O et al. Hemodynamics of focal versus global growth of small cerebral aneurysms. Clin Neuroradiol 2017. [Epub ahead of print]. doi: 10.1007/ s00062-017-0640-6.
27. Russell JH, Kelson N, Barry M et al. Computational fluid dynamic analysis of intracranial aneurysmal bleb formation. Neurosurgery 2013; 73(6): 1061 – 1068. doi: 10.1227/ NEU.0000000000000137.
28. Cebral JR, Ollikainen E, Chung BJ et al. Flow conditions in the intracranial aneurysm lumen are associated with inflammation and degenerative changes of the aneurysm wall. AJNR Am J Neuroradiol 2017; 38(1): 119 – 126. doi: 10.3174/ ajnr.A4951.
29. Penn DL, Komotar RJ, Sander Connolly E. Hemodynamic mechanisms underlying cerebral aneurysm pathogenesis. J Clin Neurosci 2011; 18(11): 1435 – 1438. doi: 10.1016/ j.jocn.2011.05.001.
30. Zhou G, Zhu Y, Yin Y et al. Association of wall shear stress with intracranial aneurysm rupture: systematic review and meta-analysis. Sci Rep 2017; 7(1): 5331. doi: 10.1038/ s41598-017-05886-w.
31. Shojima M, Oshima M, Takagi K et al. Magnitude and role of wall shear stress on cerebral aneurysm: computational fluid dynamic study of 20 middle cerebral artery aneurysms. Stroke 2004; 35(11): 2500 – 2505. doi: 10.1161/ 01.STR.0000144648.89172.0f.
32. Jou LD, Lee DH, Morsi H et al. Wall shear stress on ruptured and unruptured intracranial aneurysms at the internal carotid artery. AJNR Am J Neuroradiol 2008; 29(9): 1761 – 1767. doi: 10.3174/ ajnr.A1180.
33. Lu G, Huang L, Zhang XL et al. Influence of hemodynamic factors on rupture of intracranial aneurysms: patient-specific 3D mirror aneurysms model computational fluid dynamics simulation. AJNR Am J Neuroradiol 2011; 32(7): 1255 – 1261. doi: 10.3174/ ajnr.A2461.
34. Zhang Y, Yang X, Wang Y et al. Influence of morphology and hemodynamic factors on rupture of multiple intracranial aneurysms: matched-pairs of ruptured-unruptured aneurysms located unilaterally on the anterior circulation. BMC Neurol 2014; 14 : 253. doi: 10.1186/ s12883-014-0253-5.
35. Omodaka S, Sugiyama S, Inoue T et al. Local hemodynamics at the rupture point of cerebral aneurysms determined by computational fluid dynamics analysis. Cerebrovasc Dis 2012; 34(2): 121 – 129. doi: 10.1159/ 000339678.
36. Hejcl A, Svihlova H, Sejkorova A et al. Computational fluid dynamics of a fatal ruptured anterior communicating artery aneurysm. J Neurol Surg A Cent Eur Neurosurg 2017; 78(6): 610 – 616. doi: 10.1055/ s-0037-1604286.
37. Fukazawa K, Ishida F, Umeda Y et al. Using computational fluid dynamics analysis to characterize local hemodynamic features of middle cerebral artery aneurysm rupture points. World Neurosurg 2015; 83(1): 80 – 86. doi: 10.1016/ j.wneu.2013.02.012.
38. Hodis S, Uthamaraj S, Lanzino G et al. Computational fluid dynamics simulation of an anterior communicating artery ruptured during angiography. BMJ Case Rep 2013; 2013: pii: bcr2012010596. doi: 10.1136/ bcr-2012-010596.
39. Cebral JR, Castro MA, Burgess JE et al. Characterization of cerebral aneurysms for assessing risk of rupture by using patient-specific computational hemodynamics models. AJNR Am J Neuroradiol 2005; 26(10): 2550 – 2559.
40. Cebral JR, Hendrickson S, Putman CM. Hemodynamics in a lethal basilar artery aneurysm just before its rupture. AJNR Am J Neuroradiol 2009; 30(1): 95 – 98. doi: 10.3174/ ajnr.A1312.
41. Frosen J, Piippo A, Paetau A et al. Remodeling of saccular cerebral artery aneurysm wall is associated with rupture: histological analysis of 24 unruptured and 42 ruptured cases. Stroke 2004; 35(10): 2287 – 2293. doi: 10.1161/ 01.STR.0000140636.30204.da.
42. Schneiders JJ, Marquering HA, van den Berg R et al. Rupture-associated changes of cerebral aneurysm geometry: high-resolution 3D imaging before and after rupture. AJNR Am J Neuroradiol 2014; 35(7): 1358 – 1362. doi: 10.3174/ ajnr.A3866.
43. Sejkorova A, Dennis KD, Svihlova H et al. Hemodynamic changes in a middle cerebral artery aneurysm at follow-up times before and after its rupture: a case report and a review of the literature. Neurosurg Rev 2017; 40(2): 329 – 338. doi: 10.1007/ s10143-016-0795-7.
44. Sugiyama S, Niizuma K, Sato K et al. Blood flow into basilar tip aneurysms: a predictor for recanalization after coil embolization. Stroke 2016; 47(10): 2541 – 2547. doi: 10.1161/ STROKEAHA.116.013555.
45. Xiang J, Natarajan SK, Tremmel M et al. Hemodynamic-morphologic discriminants for intracranial aneurysm rupture. Stroke 2011; 42(1): 144 – 152. doi: 10.1161/ STROKEAHA.110.592923.
46. Janiga G, Berg P, Sugiyama S et al. The computational fluid dynamics rupture challenge 2013-phase I: prediction of rupture status in intracranial aneurysms. AJNR Am J Neuroradiol 2015; 36(3): 530 – 536. doi: 10.3174/ ajnr.A4157.
47. Berg P, Roloff C, Beuing O et al. The computational fluid dynamics rupture challenge 2013 – phase II: variability of hemodynamic simulations in two intracranial aneurysms. J Biomech Eng 2015; 137(12): 121008. doi: 10.1115/ 1.4031794.
48. van Ooij P, Guedon A, Poelma C et al. Complex flow patterns in a real-size intracranial aneurysm phantom: phase contrast MRI compared with particle image velocimetry and computational fluid dynamics. NMR Biomed 2012; 25(1): 14 – 26. doi: 10.1002/ nbm.1706.
Štítky
Dětská neurologie Neurochirurgie NeurologieČlánek vyšel v časopise
Česká a slovenská neurologie a neurochirurgie

2018 Číslo 5
-
Všechny články tohoto čísla
- Anestezie a nervosvalová onemocnění
- Nejlepší postup v terapii motoricky pokročilé Parkinsonovy nemoci je INTRADUODENÁLNÍ LEVODOPA
- Nejlepší postup v terapii motoricky pokročilé Parkinsonovy nemoci je APOMORFINOVÁ INFUZE
- Najlepší postup v terapii motoricky pokročilej Parkinsonovej nemoci je HLBOKÁ MOZGOVÁ STIMULÁCIA
- Nejlepší postup v terapii motoricky pokročilé Parkinsonovy nemoci je intraduodenální levodopa, apomorfi nová infuze nebo DBS?
- Cervikální vertigo – fikce či realita?
-
Cervikální vertigo – fikce či realita?
Komentář k článku Z. Kadaňky Jr. et al - Péče o pacienty s dysfagií po cévní mozkové příhodě v České republice
- Matematické modelování hemodynamiky mozkových aneuryzmat a možný přínos v klinické praxi z pohledu neurochirurga
- Přehled onemocnění s obrazem restrikce difuze na magnetické rezonanci mozku
- Nové poznatky v diagnostice a léčbě amyotrofické laterální sklerózy
- Léčba recidivy či rezidua multiformního glioblastomu pomocí stereotaktické radiochirurgie gama nožem – společně hodnocený soubor dvou neurochirurgických pracovišť
- Tichý akútny a subakútny mozgový infarkt u pacientov pred koronárnou intervenciou
- Vztah mezi epidemiologií a subjektivním vnímáním bolesti u pacientů se syndromem karpálního tunelu
- Umístění bifurkace bazilární tepny ve vztahu k dorsu sellae
- Validace dotazníku pro pacienty s myotonií – česká verze Myotonia Behaviour Scale
- Zrozumiteľnosť reči a klinické parametre u pacientov s Parkinsonovou chorobou
- První dokumentovaný případ japonské encefalitidy importované do České republiky
- Spinální schwannom v oblasti hrudní páteře s masivním intratumorálním krvácením
- Časná komplikace ošetření disekujícího intrakraniálního aneuryzmatu ve vertebrobazilárním povodí flow-diverterem
- Svalová dystopie ve Fallopiově kanálu
- Harvey Cushing jako kandidát Nobelovy ceny
- Stanovisko Výboru Cerebrovaskulární sekce České neurologické společnosti ČLS JEP k dlouhodobému holterovskému EKG monitoringu u pacientů s ischemickou cévní mozkovou příhodou
- Analýza dat v neurologii LXXI.<br>Pearsonův korelační koeficient
- Recenze knih
- Česká a slovenská neurologie a neurochirurgie
- Archiv čísel
- Aktuální číslo
- Informace o časopisu
Nejčtenější v tomto čísle
- Nové poznatky v diagnostice a léčbě amyotrofické laterální sklerózy
- Přehled onemocnění s obrazem restrikce difuze na magnetické rezonanci mozku
- Cervikální vertigo – fikce či realita?
- Anestezie a nervosvalová onemocnění
